правильная треугольная пирамида SABC.
R - середина ребра ВС.
S - вершина.
АВ = 7
SR = 16
Найти:S поверхности - ?
V - ?
Решение:Правильный многоугольник - многоугольник, у которого все углы и стороны равны.
Правильная пирамида - пирамида, у которой основание - правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является её высотой.
=> в основании этой правильной треугольной пирамиды лежит равносторонний △АВС.
Рассмотрим △АВС:
АВ = ВС = АС = 7, так как △АВС - равносторонний.
P△АВС = АВ + ВС + АС = 7 + 7 + 7 = 21
Так как △АВС - равносторонний => он ещё и равнобедренный.
BR = RC = 3,5, так как AR - медиана. (Также R - середина ВС, по условию)
Найдём высоту AR в △АВС, по теореме Пифагора:
с² = а² + b²
a = √c² - b²
a = √(7² - 3,5²) = √(49 - (7/2)²) = √(49 - 49/4) = √147/4 = √(147)/2 = 7√(3)/2
Итак, AR = 7√(3)/2
S осн = S △ (в основании)
S осн = S △АВС = 1/2ВС * AR = 1/2 * 7 * 7√(3)/2 = 49√(3)/4 ед.кв.
SR - высота боковой грани, так как SR - апофема.
Апофема - высота боковой грани правильной пирамиды, проведённая из её вершины.
S бок = 1/2Р * SR = 21/2 * 16 = 168 ед.кв.
S поверхности = S осн + S бок = 49√(3)/4 + 168 = 189,21762 ≈ 189 ед.кв.
Точка, на которую опущена высота SO, является серединой правильного треугольника (точка пересечения медиана).Эти медианы делятся в отношении 2:1, считая от вершины.
AR/3 - АО основания AR. (2/3)
=> AR/3 - OR основания AR (1/3)
=> OR = 1/3 * 7√(3)/2 = 7√(3)/6
Рассмотрим △SRO:
△ASO - прямоугольный, так как SO - высота.
Найдём высоту SO, по теореме Пифагора:
с² = а² + b²
a = √(c² - b²)
a = √(16² - (7√(3)/6)²) = √(256 - 49/12) = √(9069)/6
Итак SO = √(9069)/6
V = 1/3S осн * SO
V = 1/3 * 49√(3)/4 * √(9069)/6= 49√(3023)/24 ед.кб.
ответ: ≈ 189 ед.кв.; = 49√(3023)/24 ед.кб.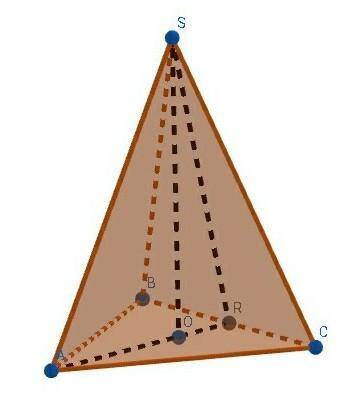
Здравствуйте!
1).
∠1+∠2=180° смежные
∠1=2∠2 по условию
2∠2+∠2=180°
3∠2=180°
∠2=60°
∠1=2∠2=120°
2). Треугольники OBC и AOD равны по двум сторонам и углу между ними (AO=OB; CO=OD по условию; ∠СОВ=AOD -вертикальные) => ∠BCO=∠ABO как соответственные углы в равных треульниках.
AD || BC, т.к. накрест лежащие углы (∠BCO=∠ABO) равны. ЧТД.
3).
AB+AC+BC=34 см. (периметр)
AB=AC (боковые стороны)
BC (основание) =АВ+2 см= АС+ 2 см
BC+ (BC + 2 см)+(ВС+2 см) =34 см
3 ВС=30 см
ВС= 10 см
АВ=АС=10 см +2 см= 12 см
4). Треугольники АОВ и DOC равны по стороне и двум прилежащим углам (АО=ОD; ∠A=∠D по условию; ∠AOB=DOC вертикальные)
5). Проведем отрезок BD. Треугольники ABD и BDC- равнобедренные (AB=AD; BC=CD по условию) => ∠АВD=∠ADB и ∠CBD=∠CDB как углы при основании в р/б треугольнике.
∠В=∠АBD+∠CBD
∠D=∠ADB+∠CDB
А так как ∠АВD=∠ADB и ∠CBD=∠CDB, то ∠В=∠D.
6). Сумма острых углов прямогульного треугольника равна 90°.
∠A+∠B=90°
∠B=∠A-60° по условию
∠A+∠A-60°=90°
2∠A=150°
∠A=75°
∠B=∠A-60°=75°-60°=15°
7). Найдем ∠B. Сумма углов треугольника равна 180°.
∠А+∠В+∠С=180°
70°+55°+∠B=180°
∠B=180°-125°
∠B=55°
То есть ∠В=∠С=55°. А если углы в треуголнике равны, то треугольник равнобедренный. Основание BC.
7.1). Рассмотрим треугольник BMC. Он прямоугольный. Сумма острых углов прямоугольного треугольника равна 90°.
∠С+∠МBC=90°
55°+∠MBC=90°
∠MBC=35°
∠ABC=∠ABM+∠MBC
55°=∠ABM+35°
∠ABM=20°