1. ∠АВС = 65°.
2. ∠АВС = 115°.
Объяснение:
Расположение точки В нам неизвестно, но предполагаем, что она находится на окружности.
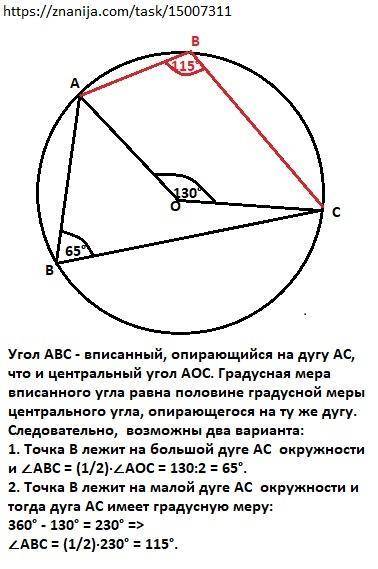
Угол АВС - вписанный, опирающийся на дугу АС, что и центральный угол АОС. Градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу. Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Следовательно, возможны два варианта:
1. Точка В лежит на большой дуге АС окружности и
∠АВС = (1/2)·∠АОС = 130:2 = 65°.
2. Точка В лежит на малой дуге АС окружности и тогда дуга АС имеет градусную меру:
360° - 130° = 230° =>
∠АВС = (1/2)·230° = 115°.
Свойства касательных:
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Следовательно:
треугольники АВО и АСО прямоугольные и равные
ВО=ОС=R
ВО=АО*Sin(ВАО)
4,5 = 9*Sin(ВАО)
Sin(ВАО) = 1/2, а это синус угла 30*
Следовательно угол ВАО=САО=30*
Угол ВАС - угол между касательными
угол ВАС=угол ВАО+угол САО=60*
ответ: угол между касательными равен 60*