(МН·РН) = 4 ед.
(ОР·РК) = -2 ед.
Объяснение:
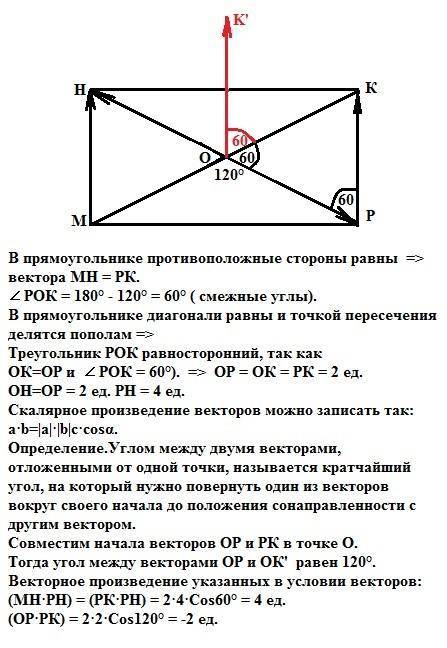
В прямоугольнике противоположные стороны равны =>
вектора МН = РК.
∠ РОК = 180° - 120° = 60° ( смежные углы).
В прямоугольнике диагонали равны и точкой пересечения делятся пополам =>
Треугольник РОК равносторонний, так как
ОК=ОР и ∠ РОК = 60°). => ОР = ОК = РК = 2 ед.
ОН=ОР = 2 ед. РН = 4 ед.
Скалярное произведение векторов можно записать так:
a·b=|a|·|b|c·сosα.
Определение: "Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором".
Совместим начала векторов ОР и РК в точке О. Тогда угол между векторами ОР и ОК' (вектора ОК и ОК' равны) равен 120°.
Векторное произведение указанных в условии векторов:
(МН·РН) = (РК·РН) = 2·4·Cos60° = 4 ед.
(ОР·РК) = 2·2·Cos120° = -2 ед.
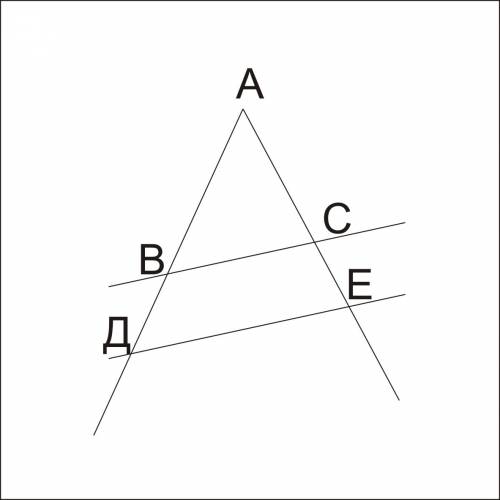
У касательных и секущих есть полезное свойство:
Если из точки вне окружности к ней проведены касательная и секущая, то
квадрат длины отрезка касательной равен произведению всего отрезка секущей
на его внешнюю часть.
Для меньшей окружности это будет
МЕ²=МА*МВ
Для большей окружности
МК²=МА*МВ
Но так как секущая для обеих окружностей одна и та же, произведение отрезка секущей на его внешнюю часть одно и то же, и
МЕ=МК, что и требовалось доказать.