6 см
Объяснение:
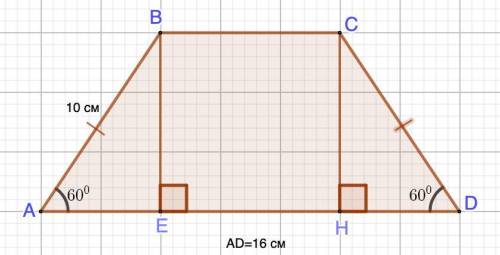
Дано: ABCD - равнобедренная трапеция.
АВ=СD=10 см; АD=16 см;
∠А=∠D=60°
Найти: АD
ВЕ и СН - высоты.
Рассмотрим ΔАВЕ - прямоугольный (построение)
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠АВЕ=90°-60°=30°
Катет, лежащий против угла в 30°, равен половине гипотенузы.
⇒АЕ = 10:2=5 (см)
Аналогично в ΔНВD:
НD=5 см
⇒ ЕН=16-(5+5)=6 (см)
Если две прямые перпендикулярны третьей, то эти прямые параллельны.
ВЕ⊥АD; СН⊥АD ⇒ВЕ║СН.
⇒ ЕВСН - параллелограмм.
У параллелограмма противоположные стороны равны.
⇒ ЕН=ВС=6 см
Самый большой угол в прямоугольном треугольнике-угол 90 градусов
Биссектриса разделила его на два равных угла
90:2=45 градусов
После проведения биссектрисы образовались два треугольника
У одного мы знаем два угла,можем узнать третий
Был треугольник АВС,проведена биссектриса СМ
В треугольнике АМС
угол АМС=74 градуса по условию задачи
угол АСМ=45 градусов
Тогда
<САМ=180-(74+45)=180-119=61 градус
Теперь рассмотрим треугольник АВС,в нем нам известны
<А=61 градус
<С=90 градусов
Сумма всех углов треугольника 180 градусов
<В=180-(61+90)=180-151=29 градусов
Треугольник СМВ
Известны 2 угла
<МСВ=45 градусов
<В=29 градусов
<СМВ=180-(45+29)=180-74=106 градусов
Объяснение:
1350
Объяснение: