Площадь треугольника можно найти по формуле S=a•h:2 , где а- основание, h- высота, проведенная к нему.
Если у треугольников равны основания и высоты, то их площади равны.
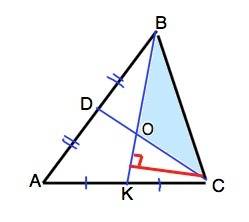
В треугольниках АВК и СВК основания АК=КС, высота из В – общая. Площади этих треугольников равны половине 0,5•SABC.
Следовательно, S ∆ ВСК=0,5 S ∆ АВС.
Рассмотрим ∆ КВС. Точка О делит ВК отношении ВО:ОК=2:1.
Это свойство точки пересечения медианы в задачах встречается нередко.
Высота для ∆ ВОС и КОС общая, поэтому площадь ∆ ВОС равна 2/3 площади ∆ КВС.
А т.к. S ∆ КВС=0,5 S ABC, то S ∆ ВОС=1/3 площади ∆ АВС.⇒
S ∆ АВС=3•S ∆ BOC=18 см²
1. вектор AB + вектор BD= вектор AC + вектор CD
2. вектор AB + вектор BC= вектор AD + вектор DC
Это правило треугольника сложения векторов: Видим что конец первого вектора совпадает с началом второго. Значит результатом сложения будет вектор, обозначенный первой буквой первого вектора и второй буквой другого вектора:
АВ + ВD = AD, AC + CD = AD
Видим, что результаты сложения совпадают, что и требовалось доказать.
Аналогично и во втором примере:
AB + BC = AC, AD + DC = АС, что и треб. доказать.
АВСD - параллелограмм
1. CA = СВ + ВА = CD + DA
2. DA = DC + CA = DB + BA
1. вектор AB + вектор BC = AC
2. вектор MN + вектор NN = MN
3. вектор PQ+ вектор QR = PR
4.вектор EF + вектор DE = DE + EF = DF
выразите вектор BC через векторы AB и AC:
BC = AC - AB
взята точка D на стороне треугольника ABC. Выразите вектор BD через векторы AB и AD:
BD = AD - AB
Дан параллелограмм ABCD. Найдите разность:
1. вектор AB- вектор AC = CB
2. вектор BC - вектор CD = AB+BC = AC
Сумма катета и удвоенного катета равна 36 см, значит катет а=36/3=12 см,
гипотенуза с=24 см.
b=√(c²-a²)=√(24²-12²)=12√3 см.