а) (-2;0) - центр окружности, радиус окружности равен 3.
б) (0; 4) - центр окружности, радиус окружности равен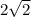 
.
в) (5; -7) - центр окружности, радиус окружности равен 4.
Объяснение:
Уравнение окружности имеет вид: (x-a)²+(y-b)²=R². Здесь центр окружности (a; b) . R - радиус окружности.
а) (-2; 0) -центр окружности, R²=9. R²=3². R=3.
б) (0; 4) - центр окружности,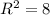 
, 
.
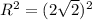
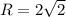в) (5; -7) - центр окружности, R²=16,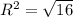 
, R=4.
Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень
а) (-2;0) - центр окружности, радиус окружности равен 3.
б) (0; 4) - центр окружности, радиус окружности равен .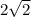
в) (5; -7) - центр окружности, радиус окружности равен 4.
Объяснение:
Уравнение окружности имеет вид: (x-a)²+(y-b)²=R². Здесь центр окружности (a; b) . R - радиус окружности.
а) (-2; 0) -центр окружности, R²=9. R²=3². R=3.
б) (0; 4) - центр окружности, , .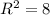
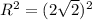
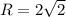в) (5; -7) - центр окружности, R²=16, 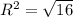, R=4.
Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень
Проведем прямую АК перпендикулярно AD (пусть К - точка пересечения АК с продолжением ВС, ясно, что АК - высота трапеции, АК = Н) и рассмотрим проекции точек K,L,P,F на эту прямую. К примеру, точка К делит отрезок, соединяющий А и середину ВС, в отношении 2/1, считая от А, поэтому её проекция на АК - пусть это точка K1, делит АК в отношении 2/1, считая от А. То есть АК1 = Н*2/3.
Аналогично AL1 = AK1 = H*2/3; AP1 = AF1 = H/3; L1, P1, F1 проекции L, P, F на АК.
Легко видеть, что проекция точки пересечения KP и LF на АК попадает в середину АК, то есть делит высоту пополам. От оснований ничего не зависит.