Объяснение:
Решается с применением теоремы: биссектриса, опущенная на сторону треугольника, делит её на отрезки в сотношением, равным отношению двух других сторон треугольника.
1)
пусть Х - длина отрезка AD:
AD = х, тогда СD = (20 - х).
Составим пропорцию по теореме:
\begin{gathered}\frac{AD}{DC}=\frac{AB}{BC}\\ \frac{x}{20-x}=\frac{10}{15}\\ 15x = 10(20-x)\\ 15x = 200-10x\\ 15x + 10x = 200\\ 25x = 200\\ x = 8\\ AD=8 \\ DC=12\\\end{gathered}
DC
AD
=
BC
AB
20−x
x
=
15
10
15x=10(20−x)
15x=200−10x
15x+10x=200
25x=200
x=8
AD=8
DC=12
2)
Составим пропорцию по теореме:
\begin{gathered}\frac{AD}{DC}=\frac{AB}{BC}\\ \frac{8}{5}=\frac{16}{BC}\\ BC = \frac{16*5}{8}\\ BC = 10\\\end{gathered}
DC
AD
=
BC
AB
5
8
=
BC
16
BC=
8
16∗5
BC=10
3)
пусть Х - длина отрезка AD:
AD = х, тогда СD = (х+1).
Составим пропорцию по теореме:
\begin{gathered}\frac{AD}{DC}=\frac{AB}{BC}\\ \frac{x}{x+1}=\frac{2}{7}\\ 7x = 2(x+1)\\ 7x = 2x+2\\ 5x = 2 \\ x = 0.4\\ AD=0.4 \\ DC=1.4\\ AC=AD+DC=0.4+1.4=1.8\\\end{gathered}
DC
AD
=
BC
AB
x+1
x
=
7
2
7x=2(x+1)
7x=2x+2
5x=2
x=0.4
AD=0.4
DC=1.4
AC=AD+DC=0.4+1.4=1.8
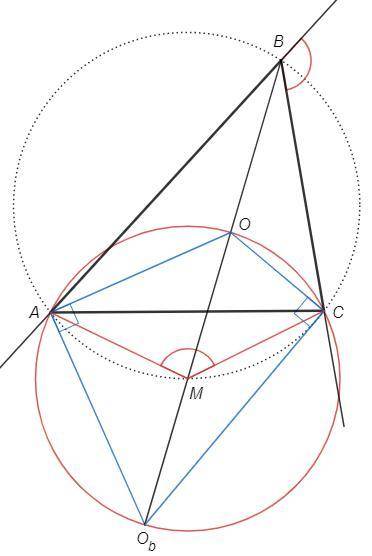
Центр вписанной окружности (O) - пересечение биссектрис внутренних углов.
Центр вневписанной окружности (Ob) - пересечение биссектрис внешних углов.
Поскольку центр Ob лежит на биссектрисах внешних углов A и С, он равноудален от прямых AB, AC, BC, следовательно лежит на биссектрисе угла B.
Биссектрисы внешнего и внутреннего углов перпендикулярны (сумма смежных углов 180, сумма их половин 90).
В четырехугольнике AOCOb противоположные углы прямые (сумма 180), следовательно он вписанный, OOb - диаметр.
Пусть M - середина OOb, центр описанной окружности AOCOb.
AMC =∪AO+∪CO =2ACO +2CAO =A+C
В четырехугольнике ABCM внешний угол равен внутреннему при противолежащей вершине, следовательно четырехугольник вписанный.
То есть M лежит на описанной окружности ABC.
не сказано, какой угол 90°, но так как АС=35, скорее всего это гипотенуза и <В=90°
По теореме Пифагора
АС²=ВС²+АВ²
АВ=√АС²-ВС²
АВ=√1225-144
АВ=√1081 см