133. а) Из точки С к плоскости а(альфа) проведены две равные наклонные CA и CB, угол между
которыми равен 60°, а угол между их про-
екциями на плоскость а(альфа) равен 90° (рису-
нок 106). Найдите угол между прямой AC
и плоскостью а(альфа).

136. Дана пирамида SABCD, боковые ребра которой равны, а основание
ABCD - квадрат, Высота SO пирамиды равна h, а высота SH боковой
грани SDC наклонена к плоскости основания под углом 45°. Найдите с
точностью до 1° угол между боковым ребром пирамиды и плоскостью
Основания

👇

Открыть все ответы

Ответ:

PashaШкипер

05.06.2020

A) Дано: конус, АВ=l, OA=OB=r, АВ - хорда, ∠BOA=60°
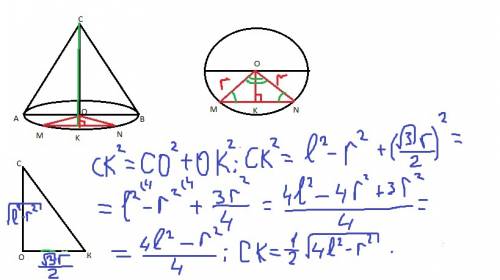
найти: S ΔAOB
Решение:
SΔ = 1/2*a*h = 1/2*AB*SK
AB= r. SK ищем из ΔАSK по т Пифагора:
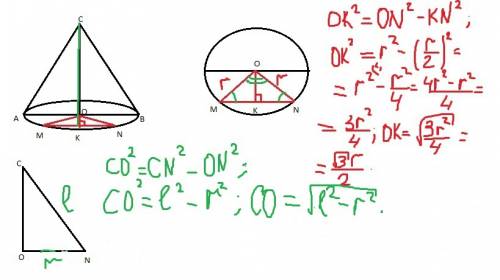
SK² = l² - (r/2)² = l² - r²/4= (4l² -r²)/4
SK = √(4l² - r²) /2
S сеч. = 1/2*r*√(4l² - r²) /2 = r*√(4l² - r²) /4
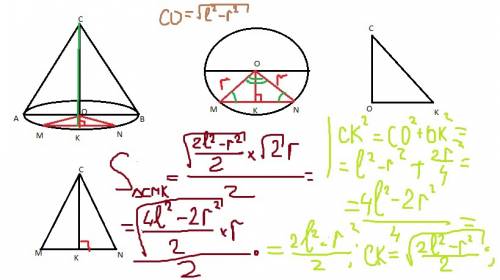
б) Дано: конус, АВ=l, OA=OB=r, АВ - хорда, ∠BOA=60°
найти: S ΔAOB
Решение :
SΔ = 1/2*a*h = 1/2*AB*SK
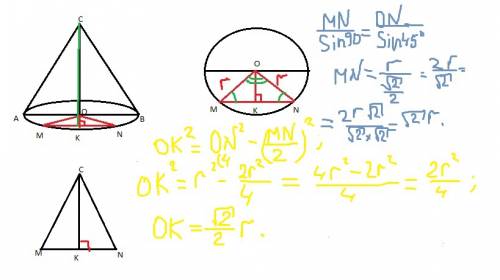
АВ ищем из ΔАВО по т. Пифагора: АВ² = r² + r² = 2r², AB = r√2
SK ищем из ΔАSK по т Пифагора:
SK² = l² - (r√2/2))² = l² -2 r²/4= (4l² -2r²)/4
SK = √(4l² -2 r²) /2
S сеч. = 1/2*r*√(4l² -2 r²) /2 = r*√(4l² -2 r²) /4

Решить : образующая конуса равна l, а радиус основания равен r. найдите площадь сечения, проходящего

Решить : образующая конуса равна l, а радиус основания равен r. найдите площадь сечения, проходящего

4,7(84 оценок)

Ответ:

Zhenechka12332145

05.06.2020

Рассмотрим основание:в образованном треугольнике MON: OM = ON как радиусы, следовательно, треугольник равнобедренный, угол MON = 60 градусов по условию, углы OMN и ONM равны как углы равнобедренного треугольника по основанию, то есть <OMN = <ONM = (180-60)/2 = 120/2 = 60 градусов. Все углы треугольника равны по 60 градусов, следовательно, треугольник - правильный, и OM = ON = MN = r. Найдем высоту ОК: из прямоугольного треугольника OKN: из теоремы Пифагора: OK^2 = ON^2 - KN^2, ON = r, KN = r/2, поскольку в правильном треугольнике высота является и медианой, OK^2 = r^2 - (r/2)^2 = r^2 - r^2/4 = 3r^2/4, OK = корень из 3 умножить на r поделить на 2. Рассмотрим треугольник CON: из теоремы Пифагора: CO^2 = CN^2 - ON^2, из вычислений на картинке CO = корень из (l^2 - r^2) поделить на два. Рассмотрим треугольник СОК: за теоремой Пифагора: CK^2 = CO^2 + OK^2, из вычислений СК = корень из (4l^2 - r^2) поделить на 2. Площадь образовавшегося сечения - это площадь треугольника CMN, которая равна стороне, умноженной на опущенную к ней высоту разделить на 2: S = CK*MN/2. S = (r*корень из ( 4l^2 - r^2)/8.
Аналогично по первому решению, во втором случае углы OMN и ONM = (180 - 90)/2 = 45 градусов. Тогда по теореме синусов: MN/sin90 = ON/sin45, MN = корень из 2 умножить на r. Из треугольника CON: CO = корень из (l^2 - r^2). Площадь второго треугольника равна r умножить на корень из (4*l^2 = 2r^2)/2) поделить на 2.

Решить : образующая конуса равна l, а радиус основания равен r. найдите площадь сечения, проходящего