10,5
Объяснение:
Дано:
a = 15
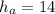
b = 20
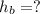
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.
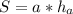
Площадь нашего одинакова, если найдем её двумя
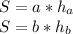
т.е.
15 * 14 = 20 * h
h = 10,5
Плоский угол при вершине правильной треугольной пирамиды равен 90°.
Найти отношение боковой поверхности этой пирамиды к площади ее основания.
Площадь правильного треугольника - а основание правильной пирамиды - правильный треугольник
S=(a²√3):4
Площадь боковой поверхности - это площадь трех граней пирамиды.
Каждая грань - равнобедренный треугольник с основанием а, равным стороне правильного треугольника в основании пирамиды, и высотой h=апофеме.
S=ah:2
Чтобы найти площадь боковой поверхности, нужно найти апофему.
Угол АSC- прямой.
Треугольник ASC - прямоугольный равнобедренный.
Апофема грани пирамиды - высота и медиана этого треугольника.
Медиана прямоугольного треугольника равна половине гипотенузы.
Высота SM равна половине АС и равна а:2
Площадь треугольника АSС=(а*а:2):2=а²:4
Площадь боковой поверхности равна 3а²:4
Отношение боковой поверхности этой пирамиды к площади ее основания
Sбок:S ᐃ АВС=(3а²:4):{(a²√3):4}=√3
ответ: 10,5см
Объяснение: Площадь параллелограмма равна произведению высоты на основание. Находим площадь по известным нам высоте и стороне. S = 14 * 15 = 210 см.
Отсюда можем найти высоту проведенную к большей стороне.
h = S/a = 210/20 = 10.5