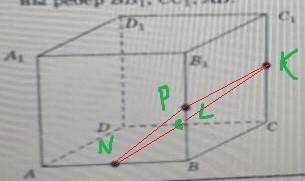
Чтобы построить сечение, проведем на нижней грани куба (см. рисунок) прямую NP║ВС, где N - середина АВ, P - середина DC. Затем соединим между собой точки N, L, K, P. В сечении получится прямоугольник NLKP.
Его площадь равна: S = NL * LK = 0,5 * AB₁ * BC = 0,5 * √2 * 1 =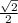 
.
AB₁ - диагональ квадрата, которая вычисляется как гипотенуза в равнобедренном прямоугольном треугольнике с катетами, равными единице. NL - средняя линия треугольника AB₁В.
ответ: площадь сечения равна 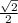квадратных единиц.
PS. На нормальном чертеже отрезки NP и KP нужно изображать пунктирными линиями, ибо они скрыты от наблюдателя снаружи куба.
1. воспользуемся тем. что скалярное произведение двух ненулевых векторов равно произведению модулей этих векторов на косинус угла между векторами. по первому рисунку IuI=√(2²+2²)*5=5√8=2*5√2=10√2; IvI=2*5=10, угол между этими векторами α=45°; поэтому скалярное произведение этих векторов равно 25*2√2*2*cos45°=25*4√2*√2/2=25*4=100
2. можно отложить от одной точки векторы →а и →m, тогда они будут одинаковы по длине, равной 2*5=10 и противоположны по направлению, т.е. угол между векторами 180°, cos180°=-1, и скалярное произведение равно
10*10*(-1)=-100
3. если же отложить от одной точки векторы →n и →d, то видим, что угол между этими векторами равен 90°, тогда скалярное произведение равно нулю, т.к. cos90°=0
ответ 1. 100; 2. -100; 3. 0