меньший катет АС=6см, больший катет ВС=12√3 см
Объяснение:
обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ. Проекции катетов на гипотенузу образует высота СН проведённая из вершины прямого угла, поэтому СН перпендикулярно АВ. СН также делит ∆АВС на 2 прямоугольных треугольника АСН и СВН в которых АН, ВН, СН - катеты, а АС и ВС - гипотенузы. Он подобны между собой, так как высота проведённая из вершины прямого угла делит его на прямоугольные треугольники подобные между собой и каждый из них подобен ∆АВС. АВ=АН+ВН=6+18=24 см. Рассмотрим ∆АСН и ∆АВС. В ∆АСН АС является гипотенузой, а в ∆АВС - гипотенуза АВ, поэтому гипотенуза АС~ гипотенузе АВ. А также меньший катет ∆АСН АН~ АС(меньшему катету ∆АВС:
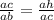
теперь подставим наши значения в эту пропорцию:
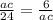
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
АС ²=6×24=144
АС=√144=12см
Теперь найдём катет ВС по теореме Пифагора:
ВС²=АВ²–АС²=24²–12²=576–144=432=12√3см

Находим объём пирамиды.
|X1 Y1 Z1| |4 3 -1|
V = (1/6)*|X2 Y2 Z2| = (1/6)*|3 2 -5|
|X3 Y3 Z3| |5 5 1| = (1/6)* 4*2*1 + 3*(-5)*5 + (-1)*3*5 -
(-1)*2*5 - 4*(-5)*5 - 3*3*1 = (1/6)*19 = 19/6.
Находим площадь треугольника АВС, лежащего против конца вектора "а". Формула векторного произведения:
Произведение векторов а × b = {aybz - azby; azbx - axbz; axby - aybx}. S(ABC) = (1/2)*b*c =
i j k
bx by bz
cx cy cz
=
i j k
3 2 -5
5 5 1
= i (2·1 - (-5)·5) - j (3·1 - (-5)·5) + k (3·5 - 2·5) =
= i (2 + 25) - j (3 + 25) + k (15 - 10) = {27; -28; 5}.
Площадь равна (1/2)√(27² + (-28)² + 5²) = (1/2)√1538 ≈ 19,60867.
Теперь находим искомое расстояние от конца вектора а до плоскости АВС как высоту пирамиды.
Н = 3V/S(ABC) = 3*(19/6)/(√1538/2) = 19/√1538 ≈ 0,48448.