В равностороннем треугольнике все углы равны 60°.
Высоты, по свойству высоты равнобедренного треугольника, являются биссектрисами и медианами, и каждая делит его на 2 равных прямоугольных треугольника.
Высота в таких треугольниках является большим катетом, который противолежит углу 60°, сторона равностороннего треугольника- гипотенузой, а меньший катет противолежит углу 30° и равен половине гипотенузы (свойство)
-----------------
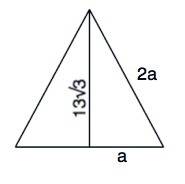
Примем меньший катет (половину стороны) равным а. Тогда гипотенуза (сторона равностороннего треугольника) равна 2а.
По т.Пифагора с²=a²+b² (с- гипотенуза, а и b- катеты)⇒
(2а)²=а²+((13√3)²⇒
3а²=13²•3 ⇒ а=13,
Сторона данного равностороннего треугольника 2а=26 (ед. длины)
или
с=b:sin60°, где с - сторона равностороннего треугольника, b- его высота.
с=(13√3):(√3/2)=26 (ед. длины)
Проведем МТ⊥АВ, МК⊥ВС, МН⊥АС. Тогда МТ = МК = МН, так как точка М равноудалена от сторон треугольника (расстояние от точки до прямой - длина перпендикуляра, опущенного из точки на прямую).
Проведем МО⊥АВС, тогда МО = 3 см, расстояние от точки М до плоскости АВС.
Соединим точку О с точками Т, К и Н. ОТ, ОК и ОН - проекции соответствующих наклонных на плоскость АВС и так же перпендикулярны сторонам треугольника по теореме, обратной теореме о трех перпендикулярах.
Если наклонные, проведенные из одной точки, равны, то равны и их проекции. Значит точка О равноудалена от сторон треугольника, и значит О - центр окружности, вписанной в треугольник АВС, ОТ = ОК = ОН = r - радиус вписанной окружности.
Sabc = pr, где р - полупериметр.
p = (AB + BC + AC) / 2 = (13 + 15 + 14) / 2 = 42 / 2 = 21 см
Найдем площадь треугольника по формуле Герона:
Sabc = √(p(p - AB)(p - BC)(p - AC))
Sabc = √(21 · (21 - 13) · (21 - 15) · (21 - 14)) = √(21 · 8 · 6 · 7) = √(3 · 7 · 4 · 2 · 2 · 3 · 7) =
= 3 · 7 · 2 · 2 = 84 см²
r = S / p = 84 / 21 = 4 см
ΔMOK: ∠MOK = 90°, по теореме Пифагора:
МК = √(МО²+ ОК²) = √(3² + 4²) = √25 = 5 см
Трапеция АВСД. АВ=СД, уголА=уголД, точка О -центр, ОВ=6,
точка М касание на АВ, ВМ/АМ=9/16, точка К касание на ВС, точка Р - касание на СД, точка Т касание на АД, АТ=АМ как касательные проведенные из одной точки и =ДТ=ДР = 16 (углаА и Д равны), по той же причине ВМ=ВК=СК=СР=9
АВ=СД=9+16=25 частей, ВС=9+9=18, АД=16+16=32, продим высоты ВН=СЛ на АД прямоугольные треугольники АВН и ЛСД равны по гипотенузе и острому углу, АН=ЛД, НВСЛ - прямоугольник ВС=НЛ=18. АН=ЛД = (АД - НД)/2 = (32-18)/2=7
Треугольник АВН, ВН = корень (АВ в квадрате - АН в квадрате) = корень (625-49)= 24
ВН = диаметру окружности, проводим радиус ОК в точку касания , радиус =24/2=12
треугольник ВКО прямоугольный ВО=корень (ВК в квадрате +ОК в квадрате) = корень(81+144)=15
ВО=15 частей = 6см
1 часть=6/15=0,4
АВ=СД=25 х 0,4 =10
ВС=18 х 0,4 = 7,2
АД=32 х 0,4 = 12,8
Периметр = 10+10+7,2+12,8=40