Поскольку фокусы гиперболы лежат на оси абсцисс симметрично относительно начала координат, то это стандартная гипербола, которая имеет уравнение:
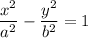, где а - действительная полуось, b - мнимая полуось
Поскольку дана точка гиперболы, то подставим ее координаты в уравнение:
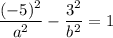
Также распишем эксцентриситет гиперболы:
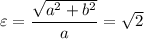
Преобразуем. Возведем в квадрат:
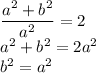
Подставим в уравнение с координатами выявленное соотношение:
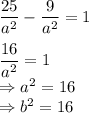
Все необходимые данные для записи уравнения есть:
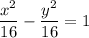
Поскольку квадрат мнимой полуоси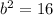 
, то ее длина - соответственно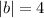 
Основная теорема, на которой базируется решение практически всех задач, звучит так: высота в равнобедренном треугольнике является биссектрисой и медианой.
Докажем , что биссектриса в равнобедренном треугольнике- это высота и медиана:
1) Биссектриса делит треугольник пополам .
2) Высота равнобедренного треугольника-это линия проведённая из вершины до противоположной стороны.
Вывод: Что биссектриса , что высота, что медиана равнобедренного треугольника являются равными и образуют 2 прямых угла при основании.
параллелограмм АВСД, высота ВК на продолжении АД, высота ВЛ на продолжении СД,
уголВ=уголД= х, уголС=уголА=180-х,
треугольник ВСЛ прямоугольный , угол ВСЛ=180 - уголС =180-(180-х)=х, уголЛВС=90-х
треугольник КВА прямоугольный, угол КАВ = 180-уголА=180-(180-х)=х, угол КВА=90-х
угол КВЛ=уголКВА+уголВ+уголЛВС=144
(90-х) + х + (90-х)=144
х=36 = уголВ=уголД
уголС=уголА=180-36=144
уголВСД=144