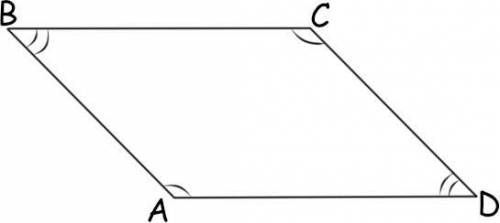
Докажите, что сумма любых двух соседних углов (углов, которые "прилегают" к одной стороне) параллелограмма равна 180°.
- - -
Параллелограмм - это четырёхугольник, у которого противоположные стороны (стороны, не имеющие общих вершин) параллельны.
На рисунке -
AB║CD, BC║AD.
Сначала рассмотрим прямые AB и CD когда они пересечены секущей СВ. Так как AB║CD (по условию), то внутренние односторонние ∡В и ∡С в сумме дают 180° (свойство односторонних углов при параллельных прямых).Теперь рассмотрим эти же прямые когда они пересечены секущей AD. Аналогично, внутренние односторонние углы ∡A и ∡D в сумме дают 180°.Теперь сделаем так.
Так как -
∡B+ ∡C = 180°
∡A + ∡D = 180°
Но также по свойству параллелограмма мы знаем, что противоположные углы параллелограмма равны (на рисунке отмечены дугами), то из выше написанного соотношения мы получаем, что -
∡A + ∡B = 180°
∡C + ∡D = 180°.
- - -
Что требовалось доказать!
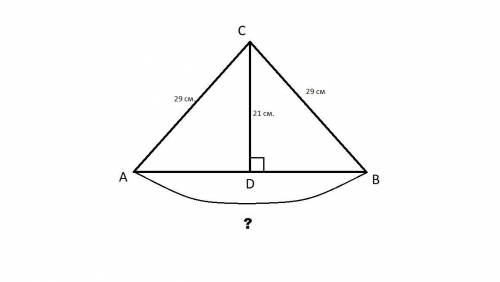
Объяснение:
треугольники ACD и DCB равны (по 2м сторонам и углу между ними):
1)общая сторона CD
2) AC и CB равны
3) углы ACD и DCB равны(высота равнобедренного треугольника, проведённая к основанию является и медианой, и биссектрисой)
Треугольники прямоугольные
По теореме Пифагора:
CB²=DC²+DB²
Из этого следует, что DB²=CB²-DC²
DB² = 400
DB = 20
AB = DB+AD= 20+20=40(DB=AB как соответственные элементы в равных треугольниках)
ответ:40