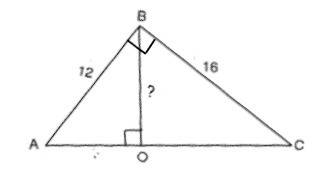
По т.Пифагора найдём гипотенузу.
АС=√(BC²+AC²)=√(256+144)=20 см
Высоту BO проще всего найти из площади треугольника.
S=BC•AB/2
S=BO•AC/2 Следовательно,
BC•AB=BO•AC, откуда
BO=BC•AB:AC
BO=16•12:20=9,6 см
-----
Вариант решения ( несколько длиннее) - его алгоритм дан ниже.
1) Находим гипотенузу по т.Пифагора
2) Катет прямоугольного треугольника – среднее пропорциональное между гипотенузой и проекцией этого катета на неё. ⇒
АВ²=АС•АО, ⇒ АО=АВ²:АС Отрезок СО находим вычитанием АО из гипотенузы или тем же что АО.
3) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу. ⇒
ВО²=СО•АО. Вычисления дадут ту же длину ВО=9,6 см
АВС - египетский треугольник (подобный тр-ку со сторонами 3,4,5), его стороны 15,20,25. Высота, проведенная к гипотенузе АВ - пусть это СН - вычисляется так
СН*25= 15*20 (это удвоенная площадь АВС, записанная СН = 12.
Плоскость DCH перпендикулярна АВ, поскольку АВ перпендикулярно DC и CH. Поэтому искомое расстояние находится из прямоугольного теругольника DCH с катетами 12 и 16. Это опять египетский треугольник, гипотенуза 20.
ответ DH = 20.
Напомню - из за того, что 3^2 + 4^2 = 5^2; подобие такому треугольнику позволяет не заниматься вычислением длинных корней, а сразу записать результат. Впрочем, кому охота, запишите теорему Пифагора и сосчитайте - результат будет тот же.