ответ: 54°
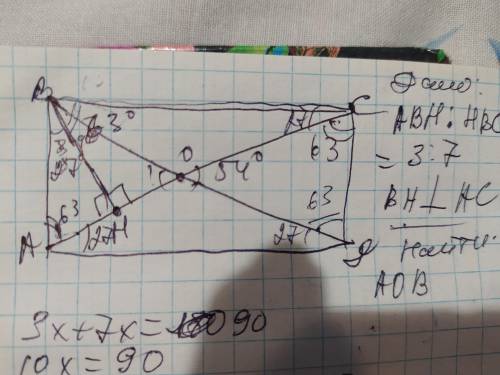
Объяснение: обозначим прямоугольник АВСД с диагональю АС и перпендикулярно ВН. Обозначим соотношение углов АВН и НВС как 3х и 7х. Зная, что они части прямого угла В, составим уравнение:
3х+7х=90
10х=90
х=90÷10
х=9
Теперь найдём части этих углов, зная х: угол АВН=3×9=27°;
Угол НВС=7×9=63°
Теперь рассмотрим полученный ∆АВН. Он прямоугольный и, зная угол ААН=27° и угол ВНА=90°, найдём угол ВАН: угол ВАН=180-27-90=63°. Рассмотрим ∆АОД. Так как в прямоугольнике диагонали, пересекаясь, делятся пополам, то этот треугольник равнобедренный: сторона АО=ОД и углы при основании равны: угол ОАД=углу ОДА. Так как угол А и угол Д полностью составляют 90°, то угол ОАД=углу ОДА=90-63=27°. Теперь найдём в этом треугольнике угол АОД: 180-27×2=180-54=126° Угол АОД=углуВОС=126°. Зная, что сумма углов в точке О составляет 360°, то сумма двух других острых углов будет составлять: 360-126×2= 360-252=108°
Так как эти углы равны, то искомый угол АОВ=углу СОД=108÷2=54°
Итак: угол АОВ=углу СОД=54°
По условию составим систему уравнений и решим ее.
b + a = 15
b - a = 9
сложим уравнения: 2b = 24; b = 12; ⇒ a = 3. Основания трапеции 12 и 3.
В трапецию вписана окружность, значит суммы противоположных сторон равны. a + b = m + n = 15.
Трапеция равнобедренная. ⇒ m = n = 15/2 = 7,5
Диаметр вписанной окружности равен высоте трапеции D = h.
В прямоугольном треугольнике гипотенуза = m = 7,5; меньший катет = (b-a)/2 = 4,5; больший катет равен высоте трапеции и диаметру вписанной окружности.
По т. Пифагора: D = h = √(7,5² - 4,5²) = 6
Диаметр вписанной окружности = 6.