Находим градусные меры дуг окружности:
360⁰:20=18⁰
бОльшая дуга=18*11=198⁰
меньшая дуга=18*9=162⁰
Известно, что вписанный угол окружности равен половине градусной меры дуги, на которую он опирается. Используя это свойство находим углы ΔМКР:
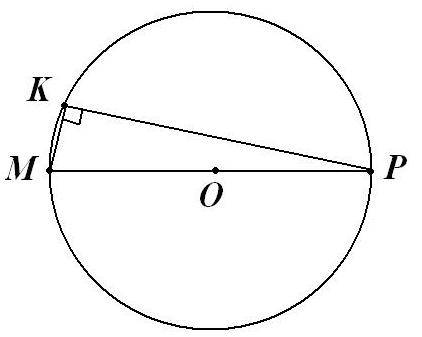
Во первых сразу можно сказать, что угол МКР- прямой, как опирающийся на диаметр:
угол МКР=180:2=90⁰
Угол МРК опирается на меньшую из двух дуг, угол МРК=162:2=81⁰
Дуга РК=180-162=18⁰, угол КМР=18:2=9⁰
Или можно найти угол КМР как 180-(90+81)=9⁰
ответ: угол МКР=90⁰
угол МРК=81⁰
угол КМР=9⁰
Ну и, как "Лучшее решение" не забывай отмечать, ОК?!... ;)
Т.к. СД-медиана, то АД=ВД. По условию ВД=АД, тогда СД=ДА=ДВ.
Значит точка Д-равноудалена от вершин треугольника АВС. То есть Д-центр описанной окружности, где отрезок АВ-диаметр. Значит вписанный угол С опирается на полуокружность, а значит, угол С=90 градусов.
Тогда угол В=90-41=49 градусов.
Треугольник АДС равнобедренный (СД=АД), поэтому угол АСД=углуСАД=41 градус.
Тогда угол ДСВ=90-41=49,
угол СДВ=180-49-49=82
ответ 49, 49 и 82 градуса