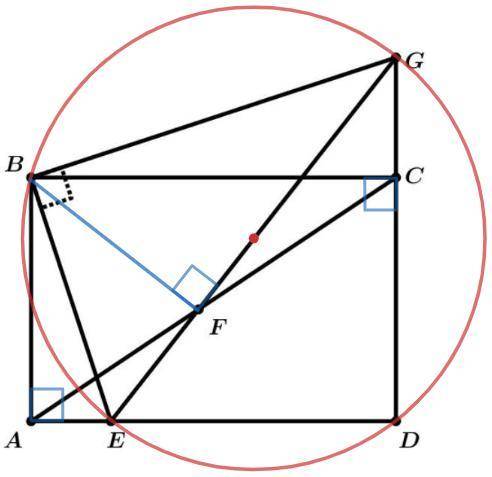
Точки A-F-C лежат на прямой Симсона точки B относительно треугольника EGD.
Объяснение:
Основания перпендикуляров, опущенных из произвольной точки описанной окружности на стороны треугольника (или их продолжения), лежат на прямой Симсона.
Точка B лежит на описанной окружности треугольника EGD (прямые углы EBG и EDG опираются на диаметр EG).
A и С - основания перпендикуляров из точки B на стороны треугольника EGD.
Тогда AC - прямая Симсона точки B относительно треугольника EGD.
(Прямая Симсона пересекает сторону EG в точке F, следовательно BF⊥EG)
Пусть в треугольнике АВС угол А равен а, угол с равен ь, проведены биссектрисы AD и СЕ, которые пересекаются в точке О (см. рисунок). Рассмотрим треугольник АОС. Сумма его углов равна 180 градусам, тогда угол АОС равен 180-1/2ВАC-1/2BCA= 180- AC - ECA = 180 - 1/2 (a+b). Угол, под которым пересекаются две прямые это наименьший из углов, которые получаются при их пересечении. Докажем, что угол ЕОА будет меньше угла АОС, тогда угол ЕОА - угол, под которым пересекаются биссектрисы. Действительно, угол ЕОА является смежным с углом АОС, тогда он равен 1/2(a+b). Так как а+ь<180, 1/2(a+b)<90 и 2(a + b) < 180 /2(a+b), то есть, какими бы ни были углы а и ь, угол ЕОА всегда будет меньше угла АОС. Окончательный ответ - 1/2(a+b).
Если провести перпендикуляры из меньшего оснавания на большее, то видно, что большее больше меньшего на 2с
Средняя линия трапеции равна (а+b)/2=(а+а+2c)=а+c
Но a+c - это катет прямоугольного треугольника, в котором диагональ - гипотенуза.
Отсюда a+c = средней линии 7 корень из 2 * cos 45 градусов
Если провести перпендикуляры из меньшего основания на большее, то видно, что большее больше меньшего на 2сСредняя линия трапеции равна (a+b)/2=(a+a+2c)/2=a+c
Но a+c- это катет прямоугольного треугольника, в котором диагональ-гипотенуза. Отсюда a+c=средней линии=10*cos 45градусов=10*(v2)/2
Примечание: v-корень, а-меньшее основание, b-большее основаниеё