18 см
Объяснение:
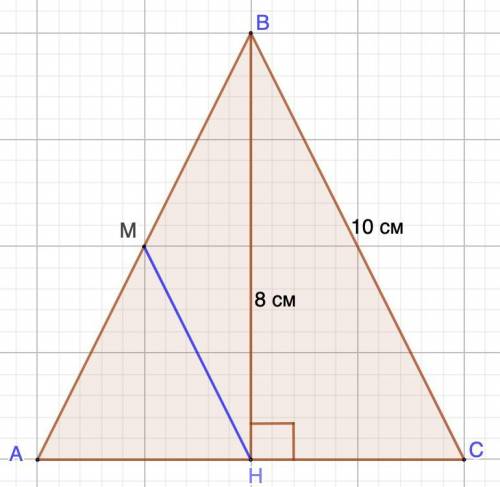
Дано: ΔАВС - равнобедренный.
ВС = 10 см;
ВН = 8 см - высота
BM || BC
Найти: Р (ΔВМН)
Рассмотрим ΔАВС - равнобедренный.
В равнобедренном треугольнике высота , проведенная к основанию, является медианой.⇒ АН = АС
НМ || ВС (условие)
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.⇒ НМ - средняя линия.
⇒ АМ = МВ = 10 : 2 = 5 (см)
Средняя линия треугольника равна половине основания.⇒ НМ = ВС : 2 = 10 : 2 = 5 (см)
Периметр равен сумме длин всех сторон.Р (ΔВМН) = МВ + ВН + МН = 5 +8 +5 = 18 (см)
1) S = 1/6
2) S = 1/2
3) S = 5/9
Объяснение:
Площадь треугольника можно вычислить по следующей формуле:
1) Обозначим площадь закрашенного ∆-ка S1 (см. рис.1)
Очевидно, т.к. точки делят стороны "единичного" ∆ка на равные отрезки, а угол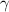 у единичного и у малого треугольника общий, то
у единичного и у малого треугольника общий, то
и площадь S1 равна
А т.к.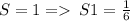
2) Пусть площадь закрашенной фигуры (а это - треугольник, см. рис.) равна S1.
Тогда площадь исходного единичного треугольника будет равна:
площадь S1, плюс общая площадь трех незакрашенных треугольников (обозначим их площади S2, S3, S4); а с учетом того, что площадь единичного треугольника равна 1:
Треугольники 2, 3, 4 - образованы точно так же, как и треугольник в первой части задачи и соответственно их площади вычисляются точно так же:
Соответственно, искомая площадь составляет
3) Пусть площадь закрашенной фигуры (а это - шестиугольник, см. рис.) равна S1
Тогда площадь исходного единичного треугольника будет равна:
площадь S1, плюс общая площадь трех незакрашенных треугольников (пусть их площади будут S2, S3, S4); а с учетом того, что площадь единичного треугольника равна 1:
Площади треугольников 2, 3 - образованы точно так же, как и треугольник в первой части задачи и соответственно их площади вычисляются точно так же:
Но площадь треугольника 4 меньше: у него две стороны втрое меньше чем у исходного единичного, потому его площадь равна:
Следовательно, общая площадь незакрашенных частей равна:
А искомая площадь закрашенной фигуры S1 составляет