Следовательно ВС = 2NF – AD = 2*20 – 14 = 40 -14 = 26 cм
Объяснение:
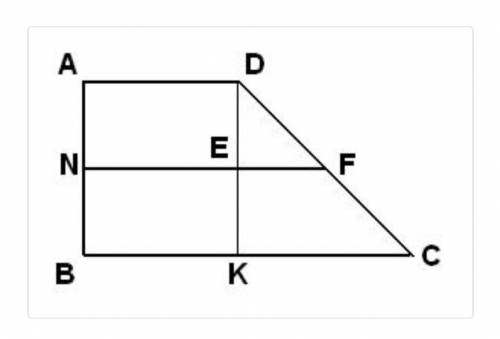
DK – перпендикуляр к ВС (см.рисунок). Так как NF - средняя линия трапеции, то AN = NB = DE = EK = AB/2 = 12/2 = 6 cм. Поскольку угол BCD = 45 градусов, то и угол NFD = 45. Тогда DE = EF = 6 см. Следовательно NE = BK = AD = NF – EF = 20 – 6 = 14 cм. В треугольнике DKC EF – его средняя линия. Посему KC = 2EF = 2*6 = 12 см. Таким образом ВС = ВК + КС. Но выше было найдено, что ВК = NE = AD = 14 см. Тогда ВС = 14 + 12 = 26 см. ВС можно было бы найти и иначе. Помните? Средняя линия трапеции равна полусумме оснований. Следовательно ВС = 2NF – AD = 2*20 – 14 = 40 -14 = 26 cм
Доказать это просто:
1) Из каждой вершины выходит n-1 отрезок к остальным n-1 вершине.
Но к двум соседним вершинам - это стороны, а не диагонали.
Поэтому из каждой вершины выходит n-3 диагонали.
Вершин всего n, поэтому получается n*(n-3) диагоналей.
2) Каждая диагональ соединяет две вершины. Если мы провели диагональ АС, то одновременно мы провели диагональ СА.
Поэтому количество диагоналей нужно разделить пополам.
Получается d = n*(n-3)/2
1) n = 4, d = 4*1/2 = 2
2) n = 5, d = 5*2/2 = 5
3) n = 6, d = 6*3/2 = 9
4) n = 10, d = 10*7/2 = 35