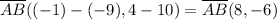 ;
; от точки A
от точки A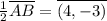 ;
; в обе возможные стороны
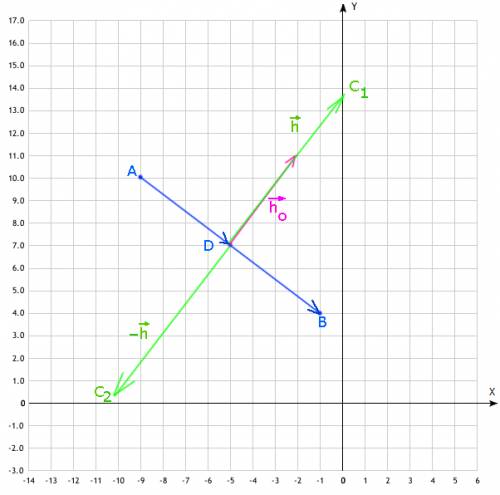
в обе возможные стороны перпендикулярен вектору основания
перпендикулярен вектору основания  , а значит его проекции накрест-пропорциональны с противоположным знаком:
, а значит его проекции накрест-пропорциональны с противоположным знаком: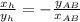 , что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:
, что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:  (II) ;
(II) ; пропорционален вектору
пропорционален вектору  , поскольку для вектора
, поскольку для вектора  выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора
выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора  ;
; имеет длину
имеет длину 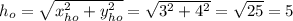 ;
;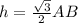 , т.к
, т.к 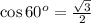 ;
;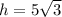 , а стало быть
, а стало быть  ;
;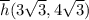 .
.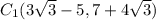 /// примечание:
/// примечание: 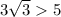 ;
;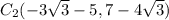 /// примечание:
/// примечание: 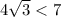 .
.
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.