
В равностороннем треугольнике АВС со стороной, равной √3, проведены три биссектрисы : AM, BH, CK. Найдите периметр треугольника ALH.
- - -
Дано :
ΔАВС - правильный (равносторонний).
АВ = √3.
АМ, ВН, СК - биссектрисы.
АМ ∩ ВН ∩ СК = L.
Найти :
Р(ΔALH) = ?
АВ = ВС = АС = √3 (по определению равностороннего треугольника).
В правильном треугольнике все его биссектрисы являются медианами и высотами.Соответственно, по определению медианы треугольника -
АН = НС = 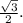
Рассмотрим ΔALH - прямоугольный (так как ∠AHL= 90° по определению высоты).
В равностороннем треугольнике все углы равны по 60°.То есть ∠А = 60°.
По определению биссектрисы треугольника -
∠ВАМ = ∠МАС = 60°/2 = 30°.
По определению косинуса острого угла прямоугольного треугольника -
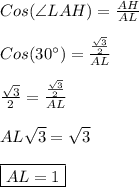
Отсюда -
LH = 0,5*AL = 1*0,5 = 0,5.
Периметр - это сумма длин всех сторон.Отсюда -
Р(ΔALH) = LH + AL + AH = 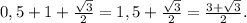
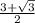 (ед).
(ед).
Задание №1
Объяснение:
Пирамида SABCD. Апофема SH - высота треугольника SAB. O - точка пересечения диагоналей основания, SO - высота пирамиды.
1) Рассмотрим прямоугольный треугольник OHS. По теореме пифагора:
OH² = SH² - SO²
OH² = 4a² - 3a²
OH = a
По теореме Фалеса: BC = 2OH = 2a
Сторона основания 2a
2) SHO - линейный угол двугранного угла SABO. Найдя его, найдем и SABO, следовательно угол между боковой гранью и основанием.
Из прямоугольного треугольника SHO:
sin<SHO = SO/SH
sin<SHO = a√3/2a = √3/2
<SHO = 60°
Угол между боковой гранью и основанием 60°
3) S = Sбок + Sосн
В основании квадрат, значит Sосн = AB² = (2a)² = 4a²
Sбок = Pосн*SH/2
Pосн = 4*2a = 8a
Sбок = 8a*2a/2 = 8a²
S = 8a² + 4a² = 12a²
Площадь 12а²
4) Из точки О (это и есть центр основания) проводим перпендикуляр к апофеме SH, обозначаем H1. SH1 - расстояние от центра основания до плоскости боковой грани.
Из прямоугольного треугольника OH1H:
sin<SHO = OH1/OH
но sin<SHO = √3/2
√3/2 = OH1/a
OH1 = a√3/2
ответы: a; 60°; 12а²; a√3/2