По условию составим систему уравнений и решим ее.
b + a = 15
b - a = 9
сложим уравнения: 2b = 24; b = 12; ⇒ a = 3. Основания трапеции 12 и 3.
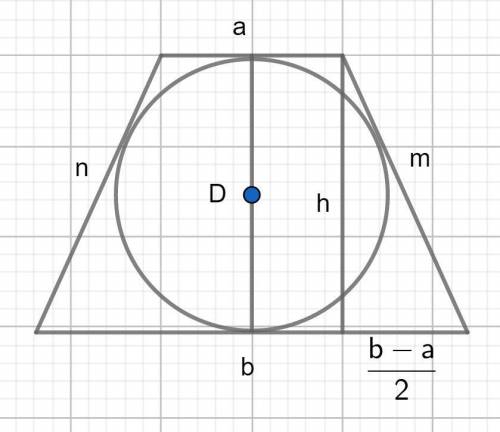
В трапецию вписана окружность, значит суммы противоположных сторон равны. a + b = m + n = 15.
Трапеция равнобедренная. ⇒ m = n = 15/2 = 7,5
Диаметр вписанной окружности равен высоте трапеции D = h.
В прямоугольном треугольнике гипотенуза = m = 7,5; меньший катет = (b-a)/2 = 4,5; больший катет равен высоте трапеции и диаметру вписанной окружности.
По т. Пифагора: D = h = √(7,5² - 4,5²) = 6
Диаметр вписанной окружности = 6.
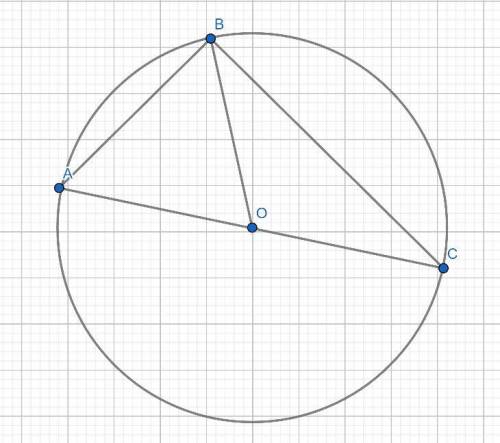
Дан прямоугольный ΔABC с прямым углом B. BO - медиана, проведенная из вершины прямого угла. Опишем около ΔABC окружность. Тогда гипотенуза AC будет являться диаметром окружности, так как вписанный угол ABC является прямым, то он опирается на диаметр окружности.
Медиана в треугольнике является отрезком, опущенным из вершины треугольника на середину противолежащей стороны. BO делит AC пополам. BO соединяет точку на окружности и центр окружности - тч.О, т.е. является радиусом окружности.
Отрезки BO = AO = OC - являются радиусами одной и той же окружности. ⇒ BO = AC/2.
Треугольник АВС, уголВ=2х, уголА=90-2х, уголС=90
от вершины А гипотенуза продлена на расстояние АС до точкиМ. треугольник АМС равнобедренный, АС=АМ, угол МАС = 180-уголСАВ=180-(90-2х)=90+2х, угол АМС=уголАСМ =(180- уголМАС)/2= (180 - 90 - 2х)/2 = 45-х
от вершины В продлеваем гипотенузу на расстояние ВС до точки К, треугольник СВК равнобедренный, ВС=ВК, угол СВК=180-уголВ=180-2х, уголВКС=уголВСК=(180-уголСВК)/2=
=(180-(180-2х))/2=х
угол МСК=уголАСМ+уголС+уголВСК=45-х+90+х=135