63гр
Объяснение:
Сумма углов тр-ка равна 180гр. Значит угол BDA = 180-47-74=59
угол CDB=180-106-58=16. Значит весь угол CDA=59+16=75
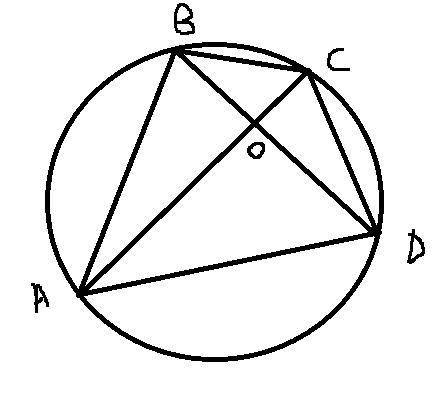
Сравниваем суммы противоположных углов четырехугольника (74+106=75+105) они равны и равны 180, значит вокруг этого четырехугольника можно описать окружность.
Для окружности верна теорема: Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.
В нашем случае дуга BC = 2*уголCDB = 32, а дуга AD = 2*угол ABD = 94.
Значит угол между диагоналями BOC=1/2*(BC+AD)=1/2*(32+94)=63.
sin a = BM/BC = 3/5 = 0,6
cos a = MC/BC = 4/5 = 0,8
tg a = BM/MC = 3/4 = 0,75
Объяснение:
Поскольку высота проведенная к основанию в равнобедреном триугольнике делит основание на две части, AM=MC=1/2AC=8/2=4 (см)
За Т. Пифагора ищем гипотенузу BC:
BC^2=BM^2+MC^2=25; BC = √25 = 5
Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе.
Отсюда sin a = BM/BC = 3/5 = 0,6
Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе.
Отсюда cos a = MC/BC = 4/5 = 0,8
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.
Отсюда tg a = BM/MC = 3/4 = 0,75