Начерти трапецию.Проведи высоту.
Рассматриваем 2 прямоугольных равнобедренных треугольника - нижний - Н (гипотенузой является нижнее основание) и верхний - В (гипотенузой является верхнее основание).
Построенный через точку пересечения диагоналей перпендикуляр к основаниям трапеции представляет собой высоту трапеции и равен сумме высот, опущенных на гипотенузу в треугольниках Н и В. Высота треугольника Н равна половине гипотенузы, т.е. половине нижнего основания трапеции (это очевидно, так как углы, прилежащие к гипотенузе равны 45 градусов). Аналогично, высота треугольника В равна половине верхнего основания трапеции.
Отсюда следует, что высота трапеции равна полусумме верхнего и нижнего оснований трапеции, т.е. ее средней линии. Значит, площадь данной трапеции равна: S = 18/2 * 18/2 = 81 см^2.
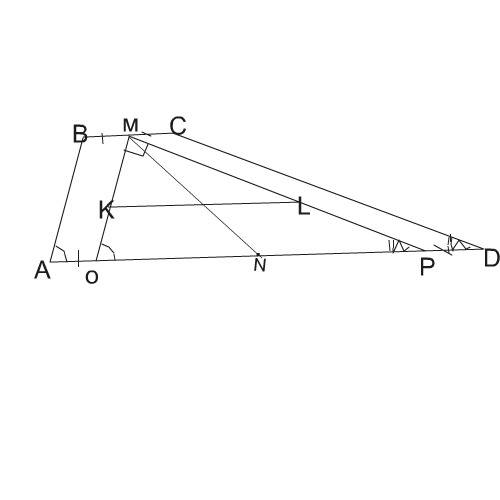
Нарсуем трапецию АВСD.
Отметим на серединах оснований трапеции точки M и N — середины оснований BC и AD соответственно.
По условию ∠A + ∠D = 90 °.
Через точку M проведём прямые, параллельные боковым сторонам трапеции AB и CD, т.е. МО║АВ и МР║СD
Точки их пересечения с основанием АD обозначим как О и Р.
По свойству углов при пересечении параллельных прямых секущей ∠МОN=∠А, ∠МРN =∠D, а ∠МОN+∠МРN=90°.
Поэтому ∠ОMР = 90 градусов.
Так как АВМО и МСDР параллелограммы по построению, АО=ВМ, РD=МС, а ВМ=МС и потому АО=РD
Кроме того,
NО = AN - AО и потому равно AN - BM и равно DN - DР =DN - CM. .
MN — медиана прямоугольного треугольника ОMР, проведённая из вершины прямого угла. По свойству медианы прямоугольного треугольника она равна половине основания этого треугольника и MN= ОN= NР.
ОР = AD - AО - РD = АD - ВМ-МС = АD - ВС.
Поэтому
MN =ОN=NР, а средняя линия KL треугольника ОМР ( что в задаче названа "вторая средняя линия")равна полуразности АD и ВС, т.е полуразности оснований.
Відповідь:
який клас
Пояснення: