Точки М i Р лежать відповідно на сторонах АB i BC трикутника АВС, АВ* РВ=СB*МB. Доведіть, що МР паралельна АC.
Объяснение:
АВ* РВ=СB*МB /: СВ*РВ ,
, .
По второму признаку подобия : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника ( ) и углы , заключённые между пропорциональными сторонами, равны ( ∠В-общий) , то такие треугольники подобны⇒ соответственные углы равны : ∠ВМР=∠ВАС. Но эти углы по расположению соответственные при секущей АВ. Значит по признаку параллельности прямых МР║АС
А) Да. Сумма смежных углов пар-грамма равна 180 градусов. Значит, сумма половин этих углов равна 90 градусов. Это и означает, что биссектрисы пересекаются под прямым углом. б) Нет. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров к сторонам. На высоте ВК он лежит, только если треугольник равнобедренный, причем В вершина, а АС основание. в) Да. В равнобедренном треугольнике точка касания вписанной окружности и основания находится в середине основания. г) Нет. Пусть внешние углы равны а и 160-а, тогда внутренние равны 180-а и 180-(160-а) = 20+а. Сумма двух внутренних углов равна 180-а + 20+а = 200 градусов. А должно быть 180 градусов в ТРЕХ углах.
Две параллельные прямые (назовём их а и b) задают плоскость Г (гамма), то есть a и b € Г. Тогда плоскость Г пересекает плоскости А(альфа) и В(бетта) по прямым АБ и А1Б1 соотвественно. По свойству номер 1 параллельных плоскостей (А//В-по усл):"Если 2 параллельные плоскости пересечены третьей, то линии их пересечения параллельны". То есть АБ//А1Б1. Теперь рассмотрим фигуру А1АББ1. В ней АБ//А1Б1(что мы уже доказали) и АА1//ББ1(по условию). Значит, фигура А1АББ1-параллелограмм по определению(противоположные стороны попарно параллельны). В параллелограмме противоположные стороны равны-это одно из его свойств. Тогда АБ=А1Б1(они противоположные)=8 см. ответ:8 см.
Точки М i Р лежать відповідно на сторонах АB i BC трикутника АВС, АВ* РВ=СB*МB. Доведіть, що МР паралельна АC.
Объяснение:
АВ* РВ=СB*МB /: СВ*РВ ,
По второму признаку подобия : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника (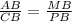 ) и углы , заключённые между пропорциональными сторонами, равны ( ∠В-общий) , то такие треугольники подобны⇒ соответственные углы равны : ∠ВМР=∠ВАС. Но эти углы по расположению соответственные при секущей АВ. Значит по признаку параллельности прямых МР║АС
) и углы , заключённые между пропорциональными сторонами, равны ( ∠В-общий) , то такие треугольники подобны⇒ соответственные углы равны : ∠ВМР=∠ВАС. Но эти углы по расположению соответственные при секущей АВ. Значит по признаку параллельности прямых МР║АС