ответ: V=54√3
Объяснение: рассмотрим полученный ∆ВВ1Д. он равнобедренный прямоугольный, поскольку угол В1ДВ=45°, а сумма острых углов прямоугольного треугольника составляет 90°, поэтому
угол ВВ1Д=90-45=45°. ВВ1 и ВД являются катетами а диагональ ВД- гипотенузой. В равнобедренном прямоугольном треугольнике катет меньше гипотенузы в √2 раз, поэтому ВВ1=ВД=6√2/√2=6. Рассмотрим ∆ВСД, он прямоугольный, ВС и СД- катеты, а диагональ ВД-гипотенуза. Угол ВДС=30°, а катет ВС, лежащий напротив него равен половине гипотенузы. Поэтому ВС=6/2=3. Найдём катет СД по теореме Пифагора:
СД²=ВД²-ВС²=6²-3³=36-9=27; СД=√27=3√3
Теперь найдём объем параллелепипеда зная его стороны и высоту по формуле:
V=длина×ширину×высоту=3×3√3×6=54√3
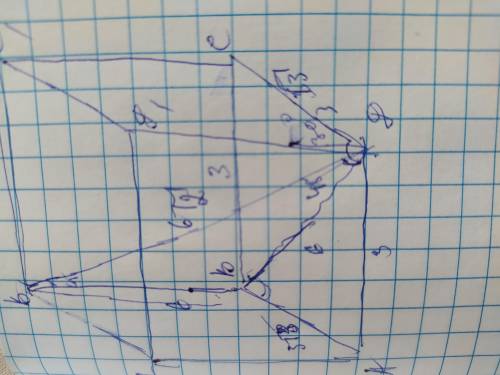
ответ: V=54√3
Объяснение: рассмотрим полученный ∆ВВ1Д. он равнобедренный прямоугольный, поскольку угол В1ДВ=45°, а сумма острых углов прямоугольного треугольника составляет 90°, поэтому
угол ВВ1Д=90-45=45°. ВВ1 и ВД являются катетами а диагональ ВД- гипотенузой. В равнобедренном прямоугольном треугольнике катет меньше гипотенузы в √2 раз, поэтому ВВ1=ВД=6√2/√2=6. Рассмотрим ∆ВСД, он прямоугольный, ВС и СД- катеты, а диагональ ВД-гипотенуза. Угол ВДС=30°, а катет ВС, лежащий напротив него равен половине гипотенузы. Поэтому ВС=6/2=3. Найдём катет СД по теореме Пифагора:
СД²=ВД²-ВС²=6²-3³=36-9=27; СД=√27=3√3
Теперь найдём объем параллелепипеда зная его стороны и высоту по формуле:
V=длина×ширину×высоту=3×3√3×6=54√3

Объяснение:
Не знаю проходили ли вы понятие серединный перпендикуляр, тогда можно было бы меньше действий в доказательстве сделать, но обойдёмся без него.
Рассмотрим △ACD. В нём AO является высотой (так как по условию AB⊥CD) и медианой (так как по условию проходит через середину стороны). Значит △ACD - равнобедренный и AC=AD.
Точно так же △BCD - равнобедренный и BC=BD.
Кроме того в треугольниках △ABC и △ABD AB - общая сторона, значит они равны по 3му признаку.