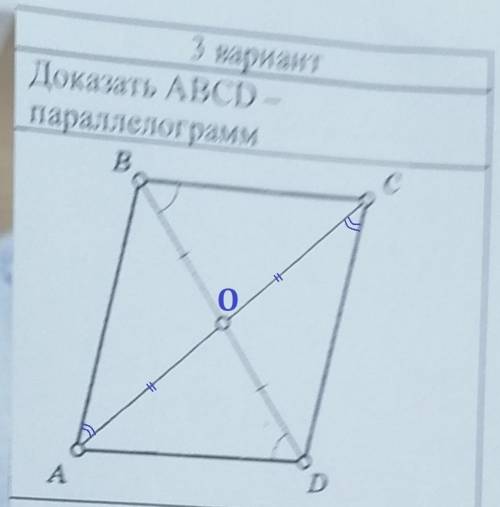
Параллелограмм - это четырехугольник, у которого противолежащие стороны попарно параллельны.
Если мы докажем, что BC║AD и AB║CD, то докажем, что ABCD параллелограмм.
1) ∠DBC = ∠BDA по условию, а это внутренние накрест лежащие углы при прямых BC и AD и секущей BD ⇒ BC║AD. (если внутренние накрест лежащие угли при двух прямых и секущей равны, то эти прямые параллельны).
2) ΔBOC = ΔAOD по второму признаку (стороне и двум углам):
BO = OD по условию, ∠OBC = ∠ODA по условию, ∠BOC = ∠AOD вертикальные углы.
В равных треугольниках соответствующие стороны равны. AO = OC
3) ΔAOB = ΔCOD по первому признаку:
BO = OD по условию, AO = OC по доказанному, ∠AOB = ∠COD - вертикальные углы.
Из равенства треугольников следует равенство соответствующих углов.
∠BAO = ∠DCO, это внутренние накрест лежащие углы при прямых AB и CD и секущей AC. ⇒ AB ║CD
4) В четырехугольнике ABCD AD║BC и AB ║ CD. Четырехугольник ABCD параллелограмм.
Доказано.
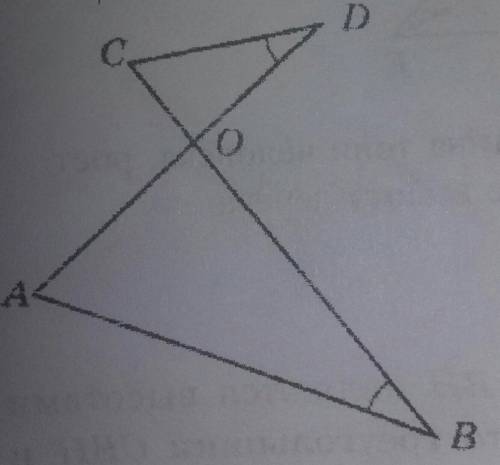
Назовём данный треугольник АВС.
ВВ1- высота к АС.
АА1=СС1 - высоты к равным боковым сторонам.
Высота равнобедренного треугольника, проведенная к основанию, является его биссектрисой и медианой. ⇒
АВ1=СВ1=30:2=15 см
∆ АВВ1=∆ СВВ1 ( по трем сторонам).
Из ∆ АВВ1 по т.Пифагора
ВВ1=√(AB²-AB1²)=√(17²-15²)=8 см
Высоты к боковым сторонам найдем из площади ∆ АВС
Заметим, что ∆ АВС - тупоугольный ( АС² > АВ²+ВС²), поэтому высоты, проведенные к боковым сторонам тупоугольного треугольника, лежат вне его.
S(ABC)=BB1•AC:2=8•15=120 см²
AA1=2S(ABC):BC
AA1=CC1=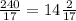 см
см