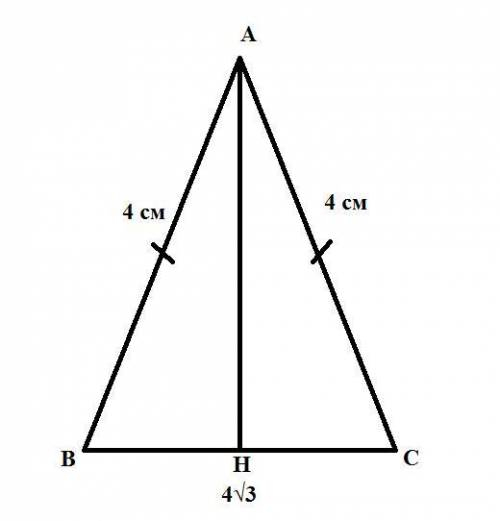
Треугольник ABC - равнобедренный. У равнобедренного треугольника углы при основании равны (∠ABC = ∠ACB) и высота (AH), проведённая с вершины (A) на основание (BC) будет делить основание пополам (BH = HC = 2√3)
Рассмотрим прямоугольный треугольник AHC (∠AHC = 90°) и найдем угол ACH с косинуса. Косинус - это отношение прилежащего катета (HC) к гипотенузе (AC), то есть:
cos ∠ACH =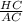 
. Подставим известные данные:
cos ∠ACH =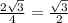 
. Значит, угол ACH = 30° (косинус 
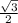равен 30°).
Угол ACH - это один из углов основания треугольника, значит второй угол при основании также будет равен 30° (∠ABC = ∠ACB = 30°)
Третий, последний угол BAC найдём из того, что сумма всех углов в треугольнике 180°, значит:
∠BAC = 180° - (30° + 30°) = 180° - 60° = 120°
ответ: ∠A = 120°; ∠B = 30°; ∠C = 30°
Известно, что |а| = 2, |b| = 3, |а + b| =√19. Вычислите:
а) Угол между векторами а и b; б) |2а - b| .
Объяснение:
a)По правилу параллелограма суммой векторов a и b будет
. Значит 
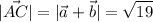
Пусть α угол между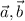
.Тогда ∠АВС=180°-α
ΔАВС, по т косинусов
АС²=АВ²+ВС²-2*АВ*ВС*cos(180-α)
19=4+9-2*2*3*(-cosα),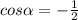
, α=120°
б) Угол между векторами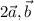
равен 120° , тк эти вектора соноправлены с векторами 
.
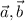Разностью векторов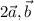
будет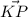 
Найдем его длину из ΔОРК по теореме косинусов КР²=ОР²+ОК²-2*ОР*ОК*cos∠РОК ,
КР²=4²+3²-2*4*3*cos120° ,
КР²=16+9-24*(-0,5) , КР=√37.