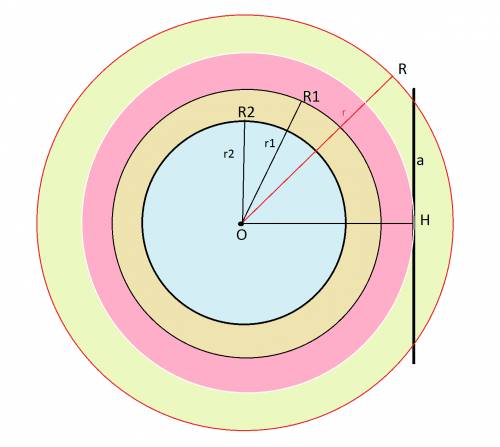
Чтобы прямая пересекала окружность, расстояние от центра окружности до прямой должно быть меньше радиуса окружности.
То есть ОН<r.
Если ОН=r, то прямая будет касаться окружности в точке Н.
Для наглядности на рисунке изображены четыре окружности разного радиуса и общим центром, из которого построен перпендикуляр к прямой. Отрезок ОН - расстояние от центра окружности до прямой.
1) Если радиус окружности r= 7 см, а расстояние ОН=9 см,
ОН>r. Прямая а не пересекает окружность с радиусом 7 см.
На рисунке такая окружность может быть желтого цвета. OR₁= 7 см
2) Если радиус окружности равен 9 см, то r=OH, и прямая касается окружности в точке Н. Розовая окружность.
3) Если радиус окружности равен 12 см, то ОН<r. И именно в этом варианте прямая пересекает окружность.
На рисунке это зеленая окружность.
4) При радиусе окружности 4,5 см, ОН>r ⇒ Прямая а не пересекает окружность. На рисунке это синяя окружность. ОR₂=4,5
ОТВЕТ: 3) Прямая пересекает окружность,если радиус окружности равен 12 см
Заклинание. Из тайной тетради... :))) Если вершина пирамиды проектируется в центр вписанной окружности, то 1. все апофемы равны 2. все грани равнонаклонены (равны двугранные уголы с основанием) 3. радиус вписанной в основание окружности И ЕСТЬ проекция апофемы на основание.
Я тут уже столько раз это объяснял, что сильно устал это делать. Всё это следует из равенства неких прямоугольных треугольников, образованных апофемами, их проекциями и высотой пирамиды. Дакажите это сами.
Площадь треугольника в основании равна 8*12/2 = 48. (некоторые товарищи спрашивают, почему 8. Это я произнес еще одно заклинание, из книги Пифагоровых чисел - 6, 8, 10. Причем 2 раза...:))
Периметр 10 + 10 + 12 = 32.
r = 48*2/32 = 3.
Еще одно заклинание, из книги Пифагоровых чисел - 3, 4, 5, и
ответ Все апофемы равны 5. :
Отнеситесь очень серьезно к этой галиматье, решение очень точное и подробное.