<Х=<36=36 градусов,как вертикальные
<Z=(180-36):3=48 градусов
<Y=<в 2 р=48•2=96 градусов
Угол,противоположный углу Z равен 48 градусов,как вертикальные
Номер 2
<Y=(180-44-62):2=74:2=37 градусов
<Z=<на 62=37+62=99 градусов,как вертикальные
<Х=<44=44 градуса,как вертикальные
Объяснение:При пересечении трёх прямых образовались три пары вертикальных углов и 3 смежных угла,вертикальные углы попарно равны,а смежные углы равны 180 градусов
В первой задаче смежный угол состоит из трёх углов
<36+<Z+<в 2 р=180 градусов
Один угол известен,мы узнаём,чему равны 2 остальных
180-36=144 градуса
И если один угол в два раза больше другого,получается,что один угол-1часть,а второй 2 части
144:3=48 градусов один угол
Второй
48•2=96 градусов
Во второй задаче тоже самое
<на 62+<Y+<44=180 градусов
Два неизвестных угла равны
180-44=136 градусов
Один угол больше другого на 62
(136-62):2=74:2=37 градусов
37+62=99 градусов
На круге размещены токчи А, В и С так, что АС - диаметр круга, а хорду ВС видно с центра окружности круга под углом в 60°. Найдите радиус круга, если АВ = 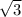 см.
см.
- - -
Дано :Круг.
Точка О - центр данного круга.
Точка А ∈кругу.
Точка В ∈кругу.
Точка С ∈кругу.
АС - диаметр круга.
∠ВОС = 60°.
АВ = 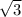 см.
см.
ОС = ? (или ОА, это неважно, так как они равны).
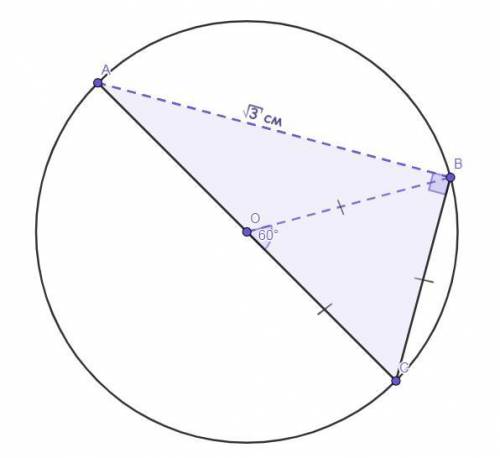
Решение :∠АВС - вписанный (по определению), так ещё и опирается на диаметр АС, следовательно, ∠АВС = 90° (так как диаметр "стягивает" дугу в 180°).
Рассмотрим ΔАВС - прямоугольный.
ОС = ОА (так как радиусы одной окружности). Тогда отрезок ОВ - медиана (по определению), причём проведённая к гипотенузе (АС - гипотенуза, так как лежит против угла в 90°).
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине.Следовательно -
ОВ = ВС = ОС.
Тогда ΔОВС - равносторонний (по определению).
Каждый угол равностороннего треугольника равен 60°.Следовательно -
∠ВОС = ∠ОВС = ∠С = 60°.
Тогда -
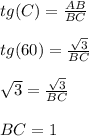
BC = 1 см.
ответ :1 см.
Найдём ВС по теореме Пифагора.ВС^2 = AB^2 - AC^2; ВС^2 = 30^2 - ( 3корня из 19)^2; ВС^2 = 900 - 9 * 19; ВС^2 = 900 - 171; ВС^2 = 729; ВС= 27; sin А = ВС : АВ = 27 : 30 = 0,9