KK₁ = 3 ед.
Объяснение:
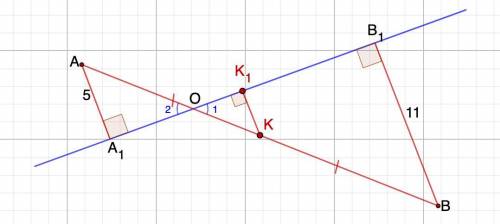
Дано: прямая АВ;
АК=КВ;
АА₁ ⊥ АВ; ВВ₁ ⊥ АВ; КК₁ ⊥ АВ.
АА₁ = 5; ВВ₁ = 11.
Найти: КК₁
Пусть А₁В₁= 2а.
Если две прямые перпендикулярны третьей, то они параллельны между собой.
АА₁ ⊥ АВ; ВВ₁ ⊥ АВ; КК₁ ⊥ АВ ⇒ АА₁ || ВВ₁ || КК₁.
Теорема Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
АК = КВ ⇒ А₁К₁ = К₁В₁ = а.
Рассмотрим ΔА₁АО и ΔОВВ₁ - прямоугольные.
Вертикальные угла равны.
∠1 = ∠2 (вертикальные)
⇒ ΔА₁АО ~ ΔОВВ₁ (по двум углам)
Составим пропорцию:
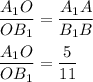
Пусть А₁О = 5х, тогда ОВ₁ = 11х
Составим уравнение:
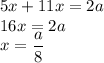
⇒ 
Тогда
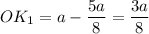
Рассмотрим ΔА₁АО и ΔК₁КО - прямоугольные.
∠1=∠2 (вертикальные)
⇒ ΔА₁АО ~ ΔК₁КО
Составим пропорцию:
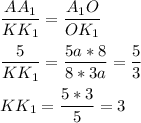
доброй ночи! я понимаю, в чём возникла трудность. но хочу вас заверить — это легко. надеюсь, вы сами это вскоре поймёте.смотрите, чтоб понять, как это делать, нам нужно вспомнить такое понятие как вектор. вектор — направленный отрезок. по условию нам даны координаты вершин треугольника авс. чтоб найти то, что от нас требуется, то первым делом, нам следует найти координаты вектора. в нашем случае — это координаты вектора ab. давайте попробуем найти координаты нужного вектора. но для этого вспомним формулу что и как делать.чтоб найти координаты вектора, надо от точки конца отнять точки начала. вот, когда мы всё это прояснили, то можем приступить к вычислению: