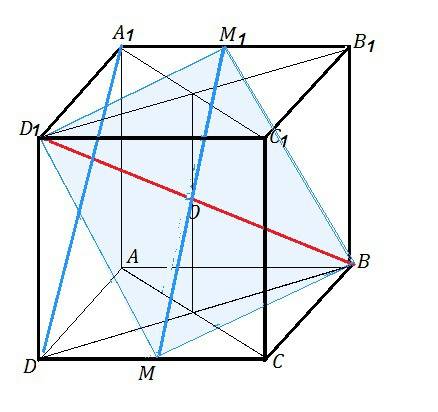
Дан куб с ребром равный 1. Найти угол между прямыми DA1 и BD1
ВD1 - диагональ куба. DА1 - диагональ его грани.
Проведем через середину диагонали куба прямую, параллельную DА1 и пересекающую ребра А1В1 и DС. Оба отрезка пересекутся в центре куба О и делятся им пополам.
Стороны четырехугольника МD1М1В равны, т.к. являются гипотенузами треугольников с равными катетами, следовательно, этот четырехугольник - ромб, и его диагонали М1М и ВD1 пересекаются под углом 90º
Найти угол между МО и ВО можно и из ∆ ВОМ по т.косинусов.
ВМ²=МО²+ВО² - 2МО•BO•cos∠BOM
cos∠BOM=(ВМ²-МО²+ВО²):(- 2МО•BO)
МО=половине диагонали грани,
ВО - половине диагонали куба.
Вычислить длины сторон ∆МОВ не составит труда. Результат решения уравнения - косинус угла ВОМ=0, и это косинус 90º
Sз.ф.=375π+25√15π см²
V=1250π см³
Объяснение:
∆АВС- прямоугольный треугольник
<АСВ=90°
АВ=40см - гипотенуза
АС=10см - катет
По теореме Пифагора найдем
ВС=√(АВ²-АС²)=√(40²-10²)=√(1600-100)=
=√1500=10√15 см.
Проведём высоту СО в ∆АВС.
СО=ВС*СА/АВ=10*10√15/40=2,5√15 см
При вращении получили два конуса.
СО=R;
Sбок(КВС)=π*CO*BC=π*2,5√15*10√15=
=375π см²
Sбок(КАС)=π*СО*АС=2,5√15*10*π=
=25√15π см²
Sз.ф=Sбок(КВС)+Sбок(КАС)=375π+25√15π см² площадь заданной фигуры.
V=⅓*Sосн*h=⅓*π*OC²*AB=
=⅓*π*(2,5√15)²*40=⅓*93,75*40π=1250π см³
4,5 см.
Объяснение:
Якщо хорди перетинаються, то добуток відрізків однієї хорди дорівнює добутку відрізків другої.
АР*ВР=РD*РC
9*2=4*РС
4РС=18
РС=4,5 см