Площадь круга, как Вы помните, находят по формуле
S=πr²
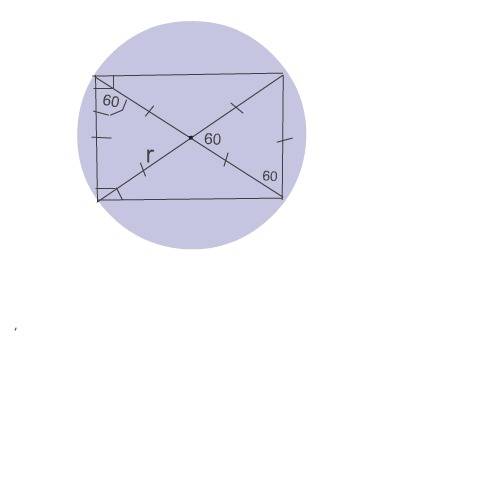
Радиус находим из остроугольных треугольников, образовавшимися диагоналями при меньшей стороне прямоугольника.
Эти треугольники - равносторонние, т.к. угол при пересечении диагоналей равен 60°, а сами диагонали делятся пополам и этим образуют равнобедренные треугольники, углы которых при основании, равном меньшей стороне вписанного прямоугольника, тоже равны 60°.⇒cледовательно, каждая половина диагонали равна меньшей стороне прямоугольника. А так как диагонали здесь являются диаметрами окружности, то радиус описанного круга тоже равен меньшей стороне прямоугольника.
r=10 см
S=πr²,
S=100 π см²
Берём параллелограмм АСВD
По свойству параллелограмма - углы, относящиеся к одной стороне дают в сумме 180 градусов, следовательно угол А + угол С = 180 градусов. Вводим величину x. Угол С (больший угол) берём за x, тогда угол А = x-82. Составляем уравнение:
x + x - 82 = 180
2x = 180 + 82
2х = 262
х = 131 - то есть угол С
угол А = х - 82 (из условия), следовательно угол А - наименьший угол - равен 131 - 82 = 49.
ответ: наименьший угол равен 49 градусам