можно было и больше поставить, задачка прикольная).. итак поехали:
стороны основания 5, 12 и 13 - это стороны прямоугольного треугольника
(25+144=169 теорема пифагора), а значит радиус вписаной окружности в основание равен р=(5+12-13)/2=2.. есть такая формула)
т.к. угол наклона у граней одинаковый, то и высоты у треугольников составляющих эти грани тоже будут одинаковы и будут составлять с высотой пирамиды и радиусом вписаной окружности в основание одинковые прямоугольные треугольники, и будут равны:
Н=корень( (4*корень(2))^2 + 2^2 ) = 6
площадь боковой поверхности пирамиды равна сумме площадей её граней, найдём каждую полупроизведением высот на их основания:
S= 5*6/2+12*6/2+13*6/2 = 15+36+39 = 90
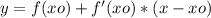
Треугольник АВС, уголВ=90
ВД=а, ДС=корень (СВ в квадрате-ВД в квадрате) =корень(4-а в квадрате)
АД /ВД =ВД/ДС, 3/а = а / корень(4-а в квадрате), возводим две части в квадрат
9 / а в квадрате = а в квадрате / 4 - а в квадрате
36 - 9а в квадрате = а в 4 степени
а в 4 степени + 9а в квадрате - 36 =0
а в квадрате = (-9 +- корень(81 + 3 х 36))/2
а в квадрате = (-9+-15) / 2 = 3
а= корень3 = ВД,
ДС = корень(4 - 3) =1
АВ= корнень (АД в квадрате+ ВД в квадрате) =корень (9+3) = 2 корень3