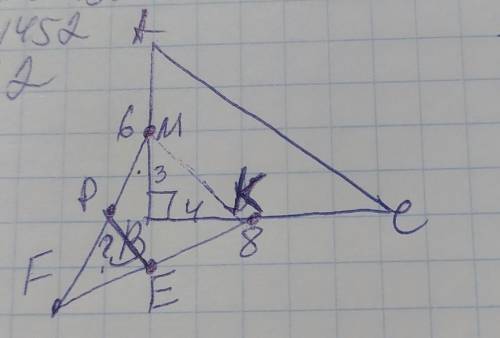
Объяснение:
Пусть точка М лежит на стороне АВ, точка К на стороне ВС, точка Р на FM, а точка Е на FK Соединим точки М и К получился отрезок МК и прямоугльный ∆ВМК, у которого с ∆АВС общий прямой угол В и ВМ и ВК - катеты, а МК - гипотенуза. Так как точки М и К взяты с середин сторон, то ВМ=6÷2=3см, а ВК=8÷2=4см. Найдём гипотенузу МК по теореме Пифагора:
МК²=ВМ²+ВК²=3²+4²=9+16=25; МК=√25=5см.
Рассмотрим полученный ∆МFE. Так как Р и Е - середины отрезков FM и FK, то РЕ параллельна МК и является её средней линией, и по свойствам средней линией треугольника РЕ=½МК=5/2=2,5см
ответ: РЕ=2,5см
Найдём угол BAC:
BAC = 180° - (30° + 105°) = 180° - 135° = 45°
По теореме синусов найдём сторону AC:
(BC)/(sinBAC) = (AC)/(sinABC);
(3√2)/(√2/2) = (AC)/(1/2);
AC = (3√2 * 1/2)/(√2/2) = 3√2 * 1/2 * 2/√2 = (3√2)/(√2) = 3 см
По той же теореме синусов найдём сторону AB:
(AC)/(sinABC) = (AB)/(sinBCA);
sin105° = sin(50+50+5) = 0.766 + 0.766 + 0.0871 = 1.6191
(3)/(1/2) = (AB)/(1.6191);
AB = (3 * 1.6191)/(1/2) = 3 * 1.6191 * 2 = 9.7146 ≈ 10 см
ответ: угол BAC = 45°; AC = 3 см; AB = 10 см