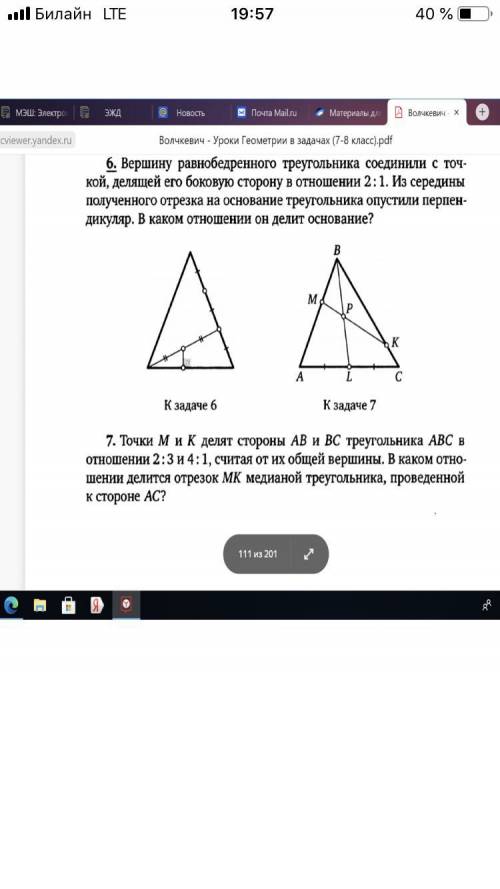
Поскольку плоскость сечения параллельна оси цилиндра, сечением будет прямоугольник с высотой H, равной высоте цилиндра, и основанием длиной L, являющемся хордой, лежащей в основании цилиндра. Также известно, что диагональ прямоугольника имеет наклон в 60 градусов к его основанию. Отсюда можно записать следующие соотношения:
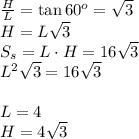
Далее проведем отрезки, соединяющие концы хорды с центром основания цилиндра. Получится равнобедренный треугольник с углом в вершине 120 градусов и бедрами, равными радиусу основания цилиндра. Проведя в этом треугольнике высоту из вешины к хорде, получим два прямоугольных треугольника, одним из катетов которых является половина хорды. Поскольку угол между этими катетами и гипотенузой равен 30 градусам, можно записать следующее соотношение между длиной хорды и радиусом основания цилиндра:
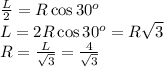
Запишем теперь выражение для площади боковой поверхности цилиндра:
ответ: Площадь боковой поверхности цилиндра равна 32пи кв. см
МН СР,МК и СТ-сходственные строны подобных треугольников МНК и СРТ.Найдите РТ и угол Н и отношение площадей подобных треугольников СРТ и МНК,если МН;СР=1:3,НК=11см,угол Р=31
находим сторону РТ:
МН/СР = НК/РТ; 1/3 = 11/х; х = 3*11:1 = 33 см. Сторона РТ = 33 см.
если треугольники подобные, то по 2 признаку подобия треугольников угол Н = углу Р = 31 градусу.
Отношение площадей 2 подобных треугольников равно квадрату коэффициента подобия.
По условию у нас коэффициент подобия = 1/3, следовательно, отношение площадей треугольников МНК/СРТ = (1:3)^2 = 1:9