
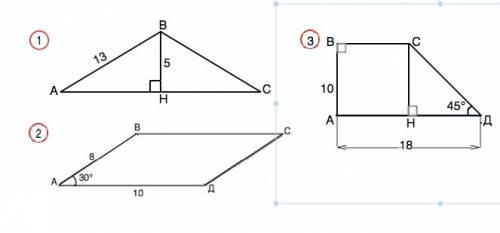
1) ОБозначим треугольник АВС, АВ=ВС=13 см, ВН=5 см.
∆ АВС равнобедренный, По свойству высоты проведенной к основанию равнобедренного треугольника, ВН= биссектриса и медиана. ⇒ АН=СН.
В ∆ АВН- отношение гипотенузы АВ и катета ВН=13:5, это треугольник из Пифагоровых троек, ⇒ АН=12 см. ( можно найти по т.Пифагора)
S (АВС)=ВН• АС:2=5•12=60 см²
* * *
2) Полное условие: В параллелограмме АВСД АВ=8 см, АД=10 см, угол ВАД=30°. Найдите площадь параллелограмма.
Одна из формул площади параллелограмма
S=a•b•sinα, где а и b соседние стороны, α - угол между ними.
S=8•10•1/2=40 см²
* * *
3) Высота данной трапеции, проведенная из вершины С тупого угла, параллельна и равна стороне АВ ( обе перпендикулярны АД)
В ∆ СНД острый угол СДН=45°, следовательно, угол ДСН=45°, ⇒ НД=СН=10 см.
В прямоугольнике АВСН сторона АН=ВС=18-10=8 см
S (АВСД)= 0,5•(АВ+АД)•СН=0,5•26•10=130 см²
Дан равнобедренный треугольник ABC, где СA = CB , А(1; -2; 1), В(3; 2; -3), точка С лежит на оси ординат. Найти стороны треугольника ABC .
ответ: |AB| = 6 ; |CA| = |CB| =3√2 ;
Объяснение: C ∈ Oy ⇒ C(0 ; y; 0)
|AB| =√ ( (3 -1)² + (2 -(-2) ) ²+( -3 -1)² ) =√ ( 4 + 16+16 ) = 6 ;
CA² = (1 - 0)²+( -2 -y)² + (1 - 0)² = 1 +( 2 +y)² + 1 = y²+4y+6
CB² = (3 - 0)²+( 2 -y)² + (-3 - 0)² =y² -4y+22 , но CA² = CB² ⇒
y²+4y+6 = y² - 4y+22 ⇔ 8y = 16 ⇒ y = 2
C(0 ; 2; 0)
|CA| =|√ ( y²+4y+6 ) =√ ( 2²+4*2*+6 ) = 3√2
* * * |CB| = √ ( y²-4y+22 ) = √ ( 2²-4*2+22 ) = 3√2 * * *