S1 ≈ 19,8 cм².
S2 ≈ 3,9 cм².
Объяснение:
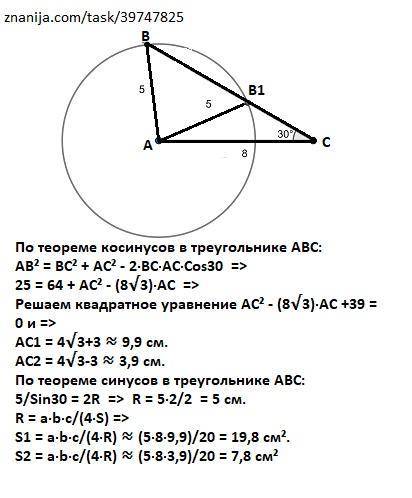
По теореме косинусов в треугольнике АВС:
АВ² = ВС² + АС² - 2·ВС·АС·Сos30 =>
25 = 64 + AC² - (8√3)·AC =>
Решаем квадратное уравнение AC² - (8√3)·AC +39 = 0 и =>
AC1 = 4√3+3 ≈ 9,9 см.
АС2 = 4√3-3 ≈ 3,9 см.
По теореме синусов в треугольнике АВС:
5/Sin30 = 2R => R = 5·2/2 = 5 см.
R = a·b·c/(4·S) =>
S1 = a·b·c/(4·R) ≈ (5·8·9,9)/20 = 19,8 cм².
S2 = a·b·c/(4·R) ≈ (5·8·3,9)/20 = 7,8 cм²
P.S. Для проверки на рисунке выполнено точное построение, доказывающее, что задача имеет два решения.
2 Чтобы найти широту, используйте горизонтальные линии, начерченные на карте – параллели. Определите, на какой параллели находится ваша точка, и найдите ее значение в градусах. Около каждой горизонтальной параллели есть обозначение в градусах (слева и справа). Если точка расположена прямо на ней, смело делайте вывод о том, что ее широта равна этому значению.
3 Если же выбранное место лежит между двумя параллелями, указанными на карте, определите широту ближайшей к нему параллели и прибавьте к ней длину дуги в градусах до точки. Длину дуги посчитайте при транспортира или примерно, на глаз. Например, если точка посередине между параллелями 30º и 35º, то ее широта будет равна 32,5º. Поставьте обозначение N, если точка расположена над экватором (северная широта) и обозначение S, если она находится под экватором (южная широта).
4 Определить долготу вам меридианы – вертикальные линии на карте. Найдите меридиан, ближе всего расположенный на карте к вашей точке и посмотрите его координаты, указанные сверху и снизу (в градусах). Измерьте с транспортира или прикиньте на глаз длину дуги между этим меридианом и выбранным местом. Прибавьте полученное расстояние в градусах к найденному значению долготы и получите долготу искомой точки.