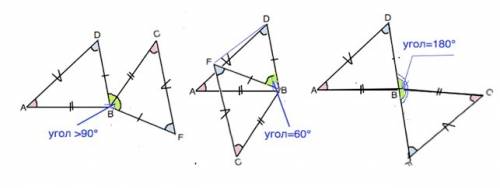
Вершина В у этих равных треугольников общая,∠D=∠F, сторона АD=CF. При наложении этих равных треугольников друг на друга вершина С совпадет с вершиной А, вершина D c F. Сторона DB=BF.
При повороте стороны CF на произвольную величину градусов ∠DBF может принимать разные значения, (см. рисунок). Поэтому, хотя DB=BF, угол DBF может быть тупым или острым ≠ 60°, и тогда ∆ DBF - равнобедренный, быть равным 60°, тогда треугольник DBF равносторонний, или BF может быть продолжением DB, тогда ∠DBF будет развернутым и треугольник DBF не получится.
ответ г.- определить невозможно.
аналогично, угол D равен 60 градусов;
опустим высоты ВЕ и СН,образовался прямоугольник, в котором ВС=ЕН=8;
АЕ=HD=(14-8)/2=3;
при этом образовавшиеся треугольники АВЕ и СНD - прямоугольные (ведь проводили высоты).
т.к. один из углов в прямоуг треугольнике равен 60, то другой, соответственно, равен 30 (сумма углов в треугольнике равна 180 градусов), т.е.
угол АВЕ=углу НСD = 30 градусов, а против угла в 30 градусов лежит катет, равный половине гипотенузы,
т.е. гипотенузы CD и AB равны
2*АЕ=2*HD=2*3=6.