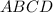 прямоугольная, то значит одна из её сторон перпендикулярна основаниям, а другая – наклонная. При этом есть две диагонали: одна идёт из прямого угла в тупой к короткому основанию, а другая – из прямого в острый к длинному основанию. Та диагональ, которая идёт к длинному основанию лежит напротив тупого угла трапеции, а значит она длиннее и короткого основания, и длинной боковой стороны (см. чертёж). Отсюда ясно, что указанная диагональ
прямоугольная, то значит одна из её сторон перпендикулярна основаниям, а другая – наклонная. При этом есть две диагонали: одна идёт из прямого угла в тупой к короткому основанию, а другая – из прямого в острый к длинному основанию. Та диагональ, которая идёт к длинному основанию лежит напротив тупого угла трапеции, а значит она длиннее и короткого основания, и длинной боковой стороны (см. чертёж). Отсюда ясно, что указанная диагональ 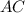 – может быть только диагональю идушей из прямого угла в тупой угол к короткому основанию. В соответствии с этим, расставим названия верщин трапеции
– может быть только диагональю идушей из прямого угла в тупой угол к короткому основанию. В соответствии с этим, расставим названия верщин трапеции 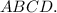 Значит,
Значит, 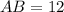 см, а
см, а 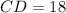 см.
см.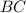 легко найти по теореме Пифагора:
легко найти по теореме Пифагора: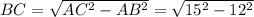 см =
см =  см
см 
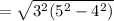 см
см 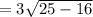 см
см 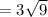 см
см 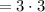 см
см 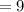 см ;
см ;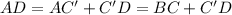 ;
;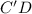 легко найти по теореме Пифагора, учитывая, что
легко найти по теореме Пифагора, учитывая, что 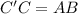 :
: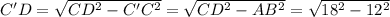 см
см 
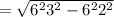 см
см 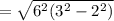 см
см 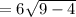 см
см 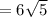 см ;
см ;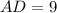 см
см 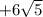 см ;
см ;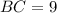 см ;
см ; 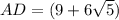 см .
см .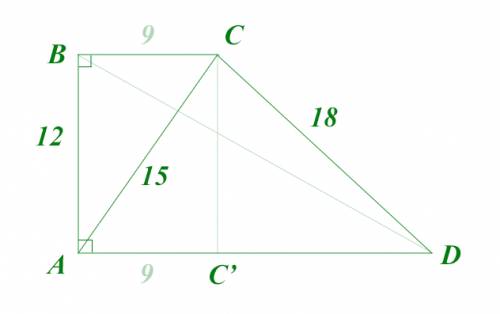
Зачем шестиугольник? Если уже дан правильный треугольник, то зная высоту, очень легко найти периметр треугольника, зная, что высота в нем является медианой. И тогда обозначив сторону за х, можно записать теорему Пифагора: х² = 81 + (х/2)². И, решая это уравнение, получаем, что х = 6√3. Откуда периметр треугольника 18√3.
Скорее всего, речь шла в задаче о периметре шестиугольника...
Если так, то нам достаточно найти радиус окружности, описанной около равностороннего треугольника R. Для шестиугольника этот радиус будет являться радиусом вписанной окружности r. Поэтому r = a√3/3 = 6 (где а - сторона треугольника)
Ну а сторона шестиугольника находится по формуле: а = 2r/√3. Значит сторона шестиугольника равна: 2*6/√3 = 4√3.
Периметр шестиугольника равен 24√3