92,8 см
Объяснение:
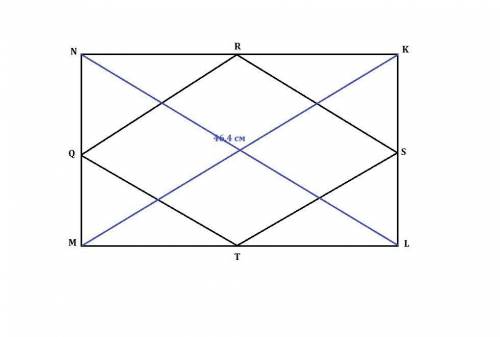
Так как MNKL - прямоугольник, то его противоположные стороны попарно равны: MN = KL, NK = ML.
Диагонали прямоугольника равны: МК=NL.
Q, R, S и T - середины сторон прямоугольника ⇒
MQ=QN=KS=SL, NR=RK=MT=TL.
Средняя линия треугольника — отрезок, который соединяет середины двух сторонQR - средняя линия ΔMNK, RS - средняя линия ΔNKL, TS-средняя линия ΔMKL, QT- средняя линия ΔNML.
Средняя линия параллельна третьей стороне, а ее длина равна половине длины этой стороныQR =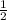 
* МК = 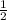* 46,4 = 23,2 см
TS = 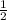* МК = 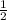* 46,4 = 23,2 см
RS = 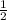* NL = 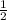* 46,4 = 23,2 см
QT = 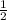* NL = 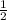* 46,4 = 23,2 см
Периметр четырёхугольника QRST:
Р=QR+TS+RS+QT=4*23,2=92,8 см
ответ:
1. р = 18см.
2 ас = 30/(√3+1) м.
объяснение:
площадь треугольника равна (1/2)·a·b·sinα, где a и b - стороны треугольника, а α - угол между этими сторонами. в нашем случае
а = 3х, b = 8x, sinα = √3/2. тогда
(1/2)·24х²·(√3/2) = 6√3 => x = 1 см.
имеем две стороны треугольника: 3см и 8см.
по теореме косинусов находим третью сторону:
х = √(3²+8²- 2·3·8·cos60) = √49 = 7см.
периметр треугольника равен 3+8+7 = 18см.
2. по теореме синусов в треугольнике авс:
ас/sinβ = ab/sinc.
∠c = 180 - 60 - 45 = 75°. sin75° = sin(45+30). по формуле
sin(45+30) = sin45·cos30 + cos45·sin30 = (√6+√2)/4.
тогда ас = ав·sinβ/sinc = (30·√3/2)/((√6+√2)/4). или
ас = 60/((√6+√2) = 60/(√2(√3+1)) = 30/(√3+1) м.