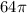 см³.
см³.
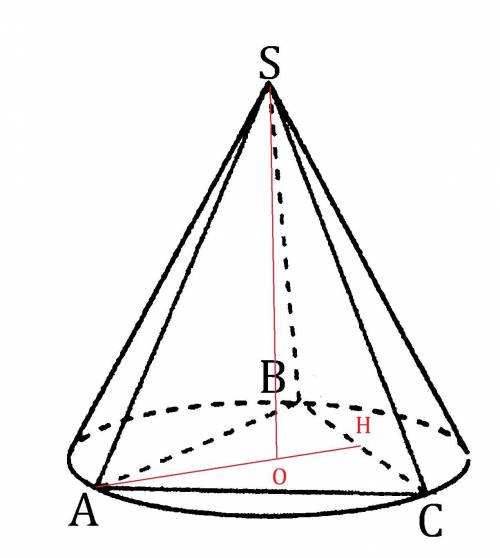
Обозначим данную пирамиду буквами 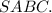
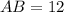 см.
см.
Проведём высоту пирамиды SO.
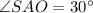
Начертим около этой пирамиды конус.
Так как конус описан около данной пирамиды, то высота конуса совпадает с высотой данной пирамиды.
=======================================================
Так как данная пирамида - правильная, треугольная ⇒ основание данной пирамиды - правильный треугольник.
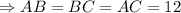 см.
см.
Проведём высоту  в
в 
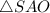 - прямоугольный, так как
- прямоугольный, так как 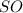 - высота пирамиды.
- высота пирамиды.
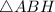 - прямоугольный, так как
- прямоугольный, так как  - высота
- высота  .
.
Так как  - равносторонний ⇒
- равносторонний ⇒  - высота, медиана и биссектриса
- высота, медиана и биссектриса
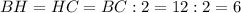 см, так как
см, так как  - медиана.
- медиана.
Найдём  по теореме Пифагора
по теореме Пифагора 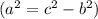 .
.
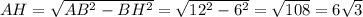 см.
см.
Точка 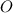 - пересечение медиан и делит их в отношении
- пересечение медиан и делит их в отношении 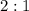 , считая от вершины.
, считая от вершины.
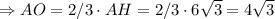 см
см
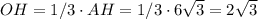 см.
см.
Также 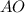 - радиус описанной около
- радиус описанной около  окружности.
окружности.
Рассмотрим 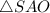
Если угол в прямоугольном треугольнике равен 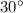 , то напротив лежащий катет равен половине гипотенузы.
, то напротив лежащий катет равен половине гипотенузы.
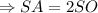
Составим уравнение:
Пусть 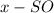 , тогда
, тогда  .
.
И по теореме Пифагора 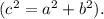
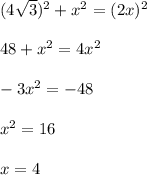
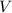 конуса =
конуса = 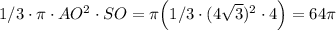 см³.
см³.
S=a×h. h - высота, a - сторона на которую опущена высота
h=sina×b. В данном случае b = 8
a) h=sin(30)×8=1/2×8=4. S=4×10=40 см²
б) h=sin(45)×8=√2/2×8=4×√2. S=4×10×√2=40√2 см²
в) h=sin(60)×8=√3/2×8=4×√3. S=4×10×√3=40√3 см²
Объяснение: