У трикутнику АВС відомо, що AB = 14 см, ВС = 21 см. На сторо- ні АВ на відстані 4 см від вершини А позначено точку D, через
яку проведено пряму, паралельну стороні АС. Знайдіть відрізки,
на які ця пряма ділить сторону BC.
А) 12 см, 9 см;
B) 15 см, 6 см;
Б) 18 см, 3 см;
Г) 14 см, 7 см.
С рисунком
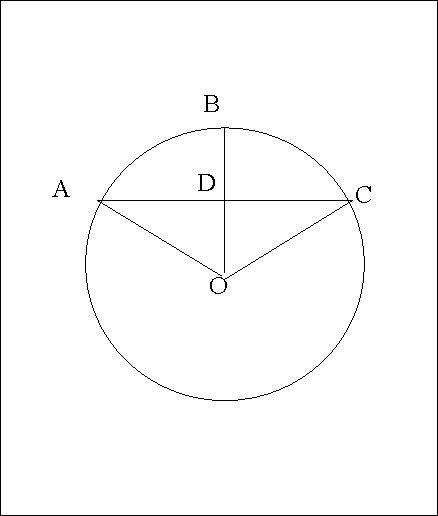
АВ=ВС
ВМ- медиана
О- точка
Доказать : треугольник АВО= треугольнику СВО.
Доказательство ;
АВ=ВС( так как , АВС - равнобедренный треугольник )
Угол В делиться ВМ пополам ( так как, медиана делит противолежащию сторону попалам => угол тоже поделился пополам).
=> треугольник АВО= треугольнику СВО ( по 1 признаку треугольников.)
Чертёж: просто начерти равнобедренный треугольник АВС , чтобы вершиной треугольника была В , Из угла В проведи медиану до стороны АС и на ней нарисуй точку О , не забудь показать черточками , что треугольник равнобедренный.
Надеюсь , что всё верно.