1
одна сторона х
другая х+4
периметр P=2*(x + x+4)=4x+8
4x+8= 24
4x=16
x=4 см
х+4=8 см
площадь S = 4*8=32 см2
ответ 32 см2
2
<C=90
<B = уголCBD=30 градусов + уголABD=60 градусов,=90 град
<A =180 - уголABD=60 градусов - уголBDA=30 градусов= 90 град
<D = 360 - <A - <B - <C=90 град
ответ в) прямоугольник
3
стороны квадрата равны - пусть b
периметр P=4b ; 16.4 =4b ; b =16.4/4=4,1 дм <---сторона
ответ 4.1 дм
Обозначим треугольник АВС, СН- высота, угол САН=55°
Сумма острых углов прямоугольного треугольника равна 90°. Значит, меньший ∠СВА=90°-55°=35°
Высота делит исходный треугольник на два прямоугольных.
АС - меньший катет. ∠САН=55°, ⇒ ∠АСН=90°-55°=35°
ВС - больший катет. ∠СВН=35°, ⇒ ∠ВСН-90°-35°=55°
Обратим внимание на то, что углы в треугольниках, на которые высота разделила∆ АВС, равны как в них, так и в исходном.
Мы получили одно из важных свойств высоты прямоугольного треугольника.
Высота в прямоугольном треугольнике, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Кроме того, каждый из этих треугольников подобен исходному.
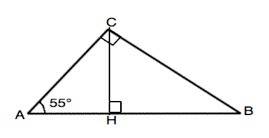
Обозначим треугольник АВС, СН- высота, угол САН=55°
Сумма острых углов прямоугольного треугольника равна 90°. Значит, меньший ∠СВА=90°-55°=35°
Высота делит исходный треугольник на два прямоугольных.
АС - меньший катет. ∠САН=55°, ⇒ ∠АСН=90°-55°=35°
ВС - больший катет. ∠СВН=35°, ⇒ ∠ВСН-90°-35°=55°
Обратим внимание на то, что углы в треугольниках, на которые высота разделила∆ АВС, равны как в них, так и в исходном.
Мы получили одно из важных свойств высоты прямоугольного треугольника.
Высота в прямоугольном треугольнике, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Кроме того, каждый из этих треугольников подобен исходному.

2(x+x+4)=24
2x+4=12
x=4
ответ площадь равна S=4*8=32
B
4a=16.4
a=4.1