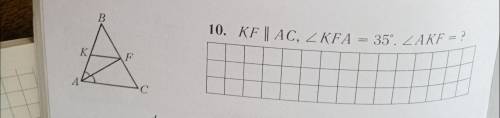
вот короче, прости за почерк

Объяснение:
общем случае, геометрическое место точек формулируется параметрическим предикатом, аргументом которого является точка данного линейного Параметры предиката могут носить различный тип. Предикат называется детерминантом геометрического места точек. Параметры предиката называются дифференциалами геометрического места точек (не путать с дифференциалом в анализе).
Роль дифференциалов во введении видовых различий в фигуру. Количество дифференциалов может быть любым; дифференциалов может и вовсе не быть.
Если заданы детерминант {\displaystyle P(M,\;a,\;b,\;c,\;\ldots )}P(M,\;a,\;b,\;c,\;\ldots ), где {\displaystyle M}M — точка, {\displaystyle a,\;b,\;c,\;\ldots }a,\;b,\;c,\;\ldots — дифференциалы, то искомую фигуру {\displaystyle A}A задают в виде: «{\displaystyle A}A — геометрическое место точек {\displaystyle M}M, таких, что {\displaystyle P(M,\;a,\;b,\;c,\;\ldots )}P(M,\;a,\;b,\;c,\;\ldots )». Далее обычно указывается роль дифференциалов, им даются названия применительно к данной конкретной фигуре. Под собственно фигурой понимают совокупность (множество) точек {\displaystyle M}M, для которых для каждого конкретного набора значений {\displaystyle a,\;b,\;c,\;\ldots }a,\;b,\;c,\;\ldots высказывание {\displaystyle P(M,\;a,\;b,\;c,\;\ldots )}P(M,\;a,\;b,\;c,\;\ldots ) обращается в тождество. Каждый конкретный набор значений дифференциалов определяет отдельную фигуру, каждую из которых и всех их в совокупности именуют названием фигуры, которая задаётся через ГМТ.
В словесной формулировке предикативное высказывание озвучивают литературно, то есть с привлечением различного рода оборотов и т. д. с целью благозвучия. Иногда, в случае детерминантов, вообще обходятся без буквенных обозначений.
Пример: параболу зададим как множество всех таких точек {\displaystyle M}M, что расстояние от {\displaystyle M}M до точки {\displaystyle F}F равно расстоянию от {\displaystyle M}M до прямой {\displaystyle l}l. Тогда дифференциалы параболы — {\displaystyle F}F и {\displaystyle l}l; детерминант — предикат {\displaystyle P(M,\;F,\;l)=(\rho (M,\;F)=\rho _{l}(M,\;l))}P(M,\;F,\;l)=(\rho (M,\;F)=\rho _{l}(M,\;l)), где {\displaystyle \rho }\rho — расстояние между двумя точками (метрика), {\displaystyle \rho _{l}}\rho _{l} — расстояние от точки до прямой. И говорят: «Парабола — геометрическое место точек {\displaystyle M}M, равноудалённых от точки {\displaystyle F}F и прямой {\displaystyle l}l. Точку {\displaystyle F}F называют фокусом параболы, а прямую {\displaystyle l}l — директрисой».
Для того что бы вычислить радиус круга необходимо знать его длину или площадь. Если нам известа одна из указаннх величин, для нас не составит труда вычислить радиус круга.
Радиус круга рассчитывается по следующим формулам:
Если нам известна длина:
Формула для расчета радиуса круга через его длину:
R=P/(2π)
Вычислить радиус круга через его длину
Если нам известна площадь:
Формула для расчета радиус круга через площадь:
R=√S/π
Вычислить радиус круга через площадь
Если нам известен диаметр:
Формула для расчета радиус круга через диаметр:
R=D/2
Вычислить радиус круга через диаметр
Где R - радиус круга, S – площадь круга, P – длина круга, D - диаметр, π – число Пи которое всегда примерно равно 3,14.
Объяснение:
И ещё.
Как вычислить площадь ( S ) круга, зная только его диаметр (D)
Например, диаметр круга = 10 сантиметров.
То радиус ( R ). естественно будет равен 5 см. ( половину диаметра )
Есть " пи " = 3,14 - это математическая постоянная, выражающая отношение окружности к длине её диаметра.
Есть формула определения площади круга ( S ):
S круга = пи х R в квадрате.
Подставляем данные в формулу:
S круга = 3,14 х ( 5 х 5 ) = 3,14 х 25 см = 78,5 квадратных см.
110
Объяснение:
Т.к. KF ║AC => ∠KFA = ∠CAF, как накрест-лежащие при секущей AF
Имеем, ∠KFA = ∠CAF = ∠KAF = 35
∠AKF = 180 - 35 - 35 = 110 (из ΔAKF)