1.
В любом треугольнике — сумма двух сторон должна быть больше оставшийся стороны, тоесть предположми, что боковые друг другу равны стороны — 7.49; 7.49, а основание — 3.74.
7.49+7.49 = 14.98 > 3.74 (сумма двух сторон больше)
3.74+7.49 = 11.23 > 7.49 (сумма двух сторон больше)
7.49+3.74 = 11.23 > 7.49.
Как мы видим, сумма каждых двух сторон больше каждой оставшийся стороны, тоесть — такой треугольник существует.
Вариант 2: боковые стороны — 3.74, основание — 7.49.
3.74+3.74 = 7.48 < 7.49.
Как мы видим сумма двух боковых сторон меньше основания, что и означает, что треугольник с боковыми сторонами 3.74; 3.74, и основанием — 7.49 — существовать не может.
2.
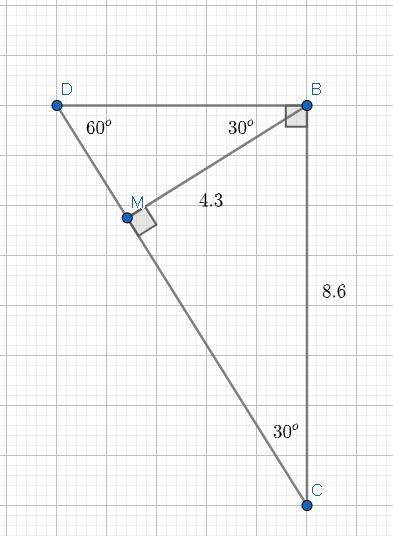
Треугольник MBC — прямоугольный треугольник, так как высота(или катет) обрзует прямой угол <BMC.
BC = 8.6; <C = 90-60 = 30° ⇒ MB = BC/2 (теорема о 30-градусном угле прямоугольного треугольника).
MB = BC/2 ⇒ MB = 8.6/2 = 4.3.
Вывод: Высота MB равна 4.3.
Объяснение:
Вариант 1
1) Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей. а) нельзя, т.к. 12>8+3 б) можно
2)18>5+5 - неверно, значит 5<18+18. Основание равно 5. Р=18+18+5=41
3) 3 4
В А D-только эти точки лежат на одной прямой
7
Вариант 2
1)Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей. а) может б) нельзя, т.к. 15>5+5
2)18>8+8 - неверно, значит 8<18+18. Основание равно 8. Р=18+18+8=44
3) 5 8
A B C-только эти точки лежат на одной прямой
13
11*12*13=1716