
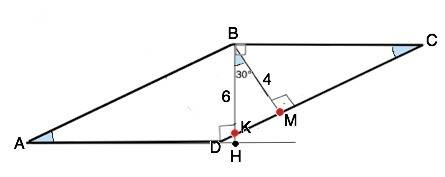
ВМ ⊥ CD, но ВН не является гипотенузой прямоугольного треугольника, образованного высотами, т.к. ВМ:ВН =4/6, и это отношение не равно cos30°
ВН пересекает СD в т.К.
∆ ВКМ - прямоугольный, угол МВК=30°, след, угол ВКМ=60°. Тогда в подобном ему по общему острому углу при К прямоугольном ∆ ВКС
угол ВСК=30°
Катет ВМ противолежит углу 30°, след. гипотенуза ВС=2 ВМ=8 см.
В параллелограмме противоположные углы равны.
След. ∠ВАН=BAD=30°, и катет ВН противолежит углу 30°, ⇒ гипотенуза АВ=2 ВН=12 см.
Площадь параллелограмма равна произведению высоты на сторону, к которой проведена.
CD=AB=12 см
S= CM•CD=4•12=48 см²
* * *
Или
Площадь параллелограмма равна произведению соседних сторон на синус угла между ними:
S=a•b•sinα
S=12•6•sin30°=96•1/2=48 см
-4х+2у=5 разделим всё на пять
-4х/5 +2у/5 =1 оставим икс и игрек в числителях
х/(-1целая1/4) +у/2,5=1 - это уравнение прямой в отрезках на
координатных осях.
Шаг 2.А теперь постройте данную прямую:
сначала оси Ох и Оу и числа положительные и отрицательные;
потом на оси Ох (горизонтальной) найдите -1целую1/4 и
обозначте точкой А;
потом на оси Оу (вертикальной) найдите 2,5 и
обозначте точкой В;
соедините прямой точки А и В, но постройте не отрезок АВ, а
прямую, то есть за пределы А и В должны выйти "хвостики".
Шаг 3.Дальше - Вы увидите на рисунке треугольник АОВ (т.О - начало координат, "перекрёсток" координатных прямых). Этот треугольник слегка заштрихуйте простым карандашом.
Шаг 4.S(площадь треугольника)=1/2 *АО*ВО=0,5 *1,25*2,5=1,5625≈1,6(кв.ед.)
ответ: 1,5625 квадратных единиц.