Сумма углов в треугольнике равна 180 градусам.
Пусть ∠В = х , тогда ∠А = 3х , ∠С = 3х + 40.
х + 3х + (3х + 40) = 180
х + 3х + 3х + 40 = 180
7х = 140
х = 20
∠В = 20°
∠А = 3 * 20 = 60°
∠С = 3 * 20 + 40 = 100°
ответ: ∠В = 20° , ∠А = 60° , ∠С = 100°.
Объяснение:
№1 фото
Условие некорректно! Скорее всего надо было найти угол С.
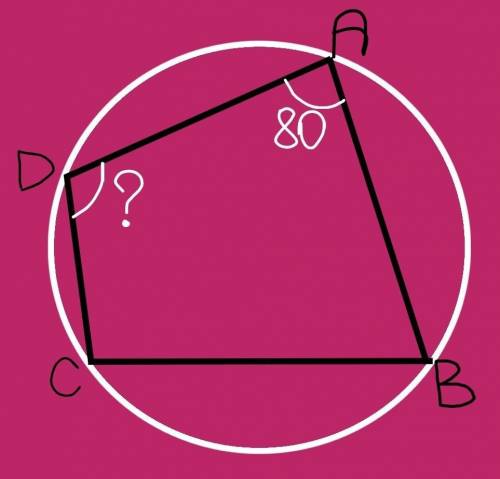
Около четырехугольника можно описать окружность, если сумма его противоположных углов равна 180°.
Углу А противоположен угол С, тогда угол С=180°–угол А=180°–80°=100°.
ответ: б) 100°
Найти угол D, незная угол В или не имея других данных, невозможно.
№2
Около четырехугольника можно описать окружность, если сумма его противоположных углов равна 180°.
Тогда угол CDA=180°–угол АВС=180°–110°=70°.
Сумма углов в любом треугольнике равна 180°.
Следовательно угол ACD=180°–угол CAD–угол CDA=180°–50°–70°=60°
ответ: в) 60°
№3
В четырехугольник можно вписать окружность, если суммы его противоположных сторон равны.
Тоесть ВС+AD=AB+CD
Пусть АВ=4n, тогда CD=3n.
Подставим значения в уравнение:
13+22=4n+3n
35=7n
n=5
Тогда CD=3*5=15 см
ответ: а) 15 см.
Если диагонали четырёхоугольника перпендикулярны, то этот четырёхугольник - ромб, а значит, все его стороны равны, т.е. АВ=ВС=СD=АD=а.
Если этот ромб вписали в окружность, то он-правильный. А правильный ромб-это квадрат.
Значит, АВСD-квадрат.
Точка О является центром окружности.
Также она является серединой пересечения диагоналей.
По теореме Пифагора находим, что ОВ= а*корень из 2 и всё поделить на 2
Пусть ОН-расстояние от точки О до стороны АВ. ВН=половине АВ= а\2
Находим ОН. Также по теореме Пифагора.
ОН= а\2
Угол А в 3 раза больше угла В
Угол А меньше угла С на 40 градусов
Найти: угол А, В, С
Решение: пусть угол В равен х градусов.
тогда угол А равен 3х и угол С = 3х + 40.
т.к. сумма этих углов = 180 градусов, составим уравнение:
Х + 3Х + 3Х + 40 = 180
7Х = 140
Х = 20
Угол А = 20*3 = 60
Угол С = 60 + 40 = 100
Угол В = 20