ответ: а) 16√3 см²; б) 4√3 см²
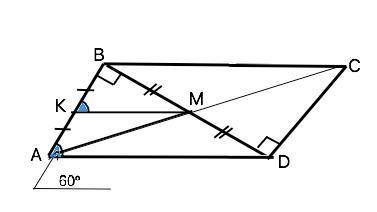
Объяснение:Диагональ BD перпендикулярна АВ ( дано), СD||АВ ⇒ BD перпендикулярна CD и делит АВСD- на два равных прямоугольных треугольника.
КМ||АD, М - середина ВD ⇒ КМ - средняя линия ∆ АВD, поэтому АD=2КМ=8 см.
Угол А=60°, ⇒ АВ=АD•cos60°=4 (см)
Площадь параллелограмма по одной из формул равна произведению соседних сторон на синус угла между ними:
Ѕ(АВСD)=4•8•√3/2=16√3 (см²)
Т.к ∆ ( АВD)=∆ DCВ, а т.М = середина ВD, отрезок АМ - медиана ∆ АВD и делит его на два равновеликих треугольника. =>
Ѕ(AMD)=S(ABCD):4=16√3:4=4√3см²
ответ: ниже
Объяснение: На фото рисунок и используемые теоремы (синусов и косинусов)
Чтобы найти сторону ВС, воспользуемся второй
cos110º= -0,342
BC=√(АС²+ВA²-2*AC*BA*cosA)=
=√(10²+6²+2*10*6*0,342)=
=√(100+36+41,04)=√(100+36+41,04)=13,3 (округлено)
sin110º=0,94
По теореме синусов находим синус одного из неизвестных углов
AC/sinB=BC/sin110º
sinB=AC*sin110º/BC=
=10*0,94/13,3= 0,707 округлено => <В=45º приблизительно
Зная, что сумма всех углов треугольника равна 180º, сожем найти и третий угол
<С=180º-110º-45º=25º